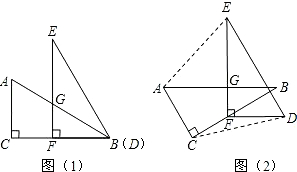
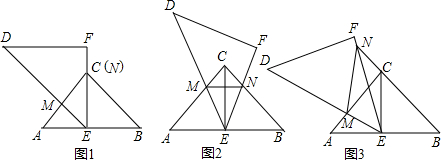
题目内容
已知两个全等的等腰直角![]() 、△DEF,其中
、△DEF,其中![]() ACB=
ACB=![]() DFE=90
DFE=90![]() ,E为AB中
,E为AB中
点,△DEF可绕顶点E旋转,线段DE,EF分别交线段CA,CB(或它们所在直线)于
M、N.
(1)如图l,当线段EF经过![]() 的顶点C时,点N与点C重合,线段DE交AC
的顶点C时,点N与点C重合,线段DE交AC
于M,求证:AM=MC;
(2)如图2,当线段EF与线段BC边交于N点,线段DE与线段AC交于M点,连
MN,EC,请探究AM,MN,CN之间的等量关系,并说明理由;
(3)如图3,当线段EF与BC延长线交于N点,线段DE与线段AC交于M点,连
MN,EC,请猜想AM,MN,CN之间的等量关系,不必说明理由。
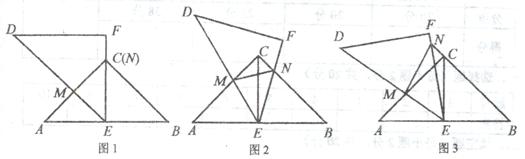
(1)∵AC=BC,E为AB中点
![]() CE⊥AB, ∠ACE=∠BCE =
CE⊥AB, ∠ACE=∠BCE =![]() ACB=45o
ACB=45o
![]() ∠AEC=90o
∠AEC=90o
![]() ∠A=∠ACE=45o
∠A=∠ACE=45o
![]() AE=CE
AE=CE
∵DF=EF, ∠DFE=90o
![]() ∠FED=45o
∠FED=45o
![]() ∠FED=
∠FED=![]() ∠AEC
∠AEC
又∵AE=CE
![]() AM=MC
AM=MC
(2)AM=MN+CN,理由如下:
在AM截取AH,使得AH=CN,连接BH
由(1)知AE=CE,∠A=∠BCE=45o
在![]() 与
与![]() 中:
中:
![]()
![]() ≌
≌![]()
![]() HE=NE,∠AEH=∠CEN
HE=NE,∠AEH=∠CEN
![]() ∠HEM=∠AEC-∠AEH-MEC=∠AEC-∠CEN-MEC=∠AEC-∠MEF=
∠HEM=∠AEC-∠AEH-MEC=∠AEC-∠CEN-MEC=∠AEC-∠MEF=![]() =45o
=45o
![]() ∠HEM=∠NEM=45o
∠HEM=∠NEM=45o
在![]() 与
与![]() 中:
中:
![]()
![]() ≌
≌![]()
![]() HM=MN
HM=MN
![]() AM=AH+HM= CN +MN
AM=AH+HM= CN +MN
即AM=MN+CN
(3)猜得MN = AM +CN

练习册系列答案
相关题目