题目内容
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.求△ABC的面积.
分析:观察图形可以发现S△ABC=S正方形AEFD-S△AEB-S△BFC-S△CDA,所以求△ABC的面积,分别求S正方形AEFD、S△AEB、S△BFC、S△CDA即可解题.
解答:解:由题意知,小四边形分别为小正方形,所以B、C为EF、FD的中点,
S△ABC=S正方形AEFD-S△AEB-S△BFC-S△CDA,
=2×2-
×1×2-
×1×1-
×1×2,
=
.
答:△ABC的面积为
.
S△ABC=S正方形AEFD-S△AEB-S△BFC-S△CDA,
=2×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
答:△ABC的面积为
| 3 |
| 2 |
点评:本题考查了直角三角形面积的计算,正方形各边相等的性质,本题中,正确的运用面积加减法计算结果是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
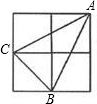 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.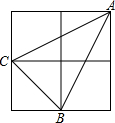 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为 如图,小正方形边长为1,则△ABC中AC边上的高等于
如图,小正方形边长为1,则△ABC中AC边上的高等于