题目内容
如图,P为边长为2的正三角形中任意一点,连接PA、PB、P C,过P点分别做三边的垂线,垂足分别为D、E、F,则PD+PE+PF= ;阴影部分的面积为 .
【答案】分析:(1)求出等边三角形的高,再根据△ABC的面积等于△PAB、△PBC、△PAC三个三角形面积的和,列式并整理即可得到PD+PE+PF等于三角形的高;
(2)因为点P是三角形内任意一点,所以当点P为三角形的中心时,阴影部分的面积等于三角形面积的一半,求出△ABC的面积,即可得到阴影部分的面积.
解答:解:(1)∵正三角形的边长为2,
∴高为2×sin60°= ,
,
∴S△ABC= ×2×
×2× =
= ,
,
∵PD、PE、PF分别为BC、AC、AB边上的高,
∴S△PBC= BC•PD,S△PAC=
BC•PD,S△PAC= AC•PE,S△PAB=
AC•PE,S△PAB= AB•PF,
AB•PF,
∵AB=BC=AC,
∴S△PBC+S△PAC+S△PAB= BC•PD+
BC•PD+ AC•PE+
AC•PE+ AB•PF=
AB•PF= ×2(PD+PE+PF)=PD+PE+PF,
×2(PD+PE+PF)=PD+PE+PF,
∵S△ABC=S△PBC+S△PAC+S△PAB,
∴PD+PE+PF= ;
;
(2)∵点P是三角形内任意一点,
∴当点P是△ABC的中心时,阴影部分的面积等于△ABC面积的一半,
即阴影部分的面积为 S△ABC=
S△ABC= .
.
故答案为: ,
, .
.
点评:本题主要利用等边三角形三边相等的性质和三角形的面积等于被分成的三个三角形的面积的和求解;第二问体现了数学问题中由一般到特殊的解题思想.
(2)因为点P是三角形内任意一点,所以当点P为三角形的中心时,阴影部分的面积等于三角形面积的一半,求出△ABC的面积,即可得到阴影部分的面积.
解答:解:(1)∵正三角形的边长为2,

∴高为2×sin60°=
 ,
,∴S△ABC=
 ×2×
×2× =
= ,
,∵PD、PE、PF分别为BC、AC、AB边上的高,
∴S△PBC=
 BC•PD,S△PAC=
BC•PD,S△PAC= AC•PE,S△PAB=
AC•PE,S△PAB= AB•PF,
AB•PF,∵AB=BC=AC,
∴S△PBC+S△PAC+S△PAB=
 BC•PD+
BC•PD+ AC•PE+
AC•PE+ AB•PF=
AB•PF= ×2(PD+PE+PF)=PD+PE+PF,
×2(PD+PE+PF)=PD+PE+PF,∵S△ABC=S△PBC+S△PAC+S△PAB,
∴PD+PE+PF=
 ;
;(2)∵点P是三角形内任意一点,
∴当点P是△ABC的中心时,阴影部分的面积等于△ABC面积的一半,
即阴影部分的面积为
 S△ABC=
S△ABC= .
.故答案为:
 ,
, .
.点评:本题主要利用等边三角形三边相等的性质和三角形的面积等于被分成的三个三角形的面积的和求解;第二问体现了数学问题中由一般到特殊的解题思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
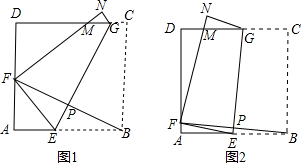 下一个正确结论(或结果):
下一个正确结论(或结果):

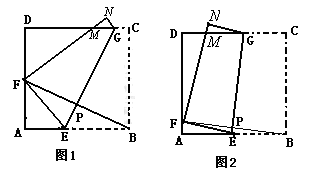
 下一个正确结论(或结果):
下一个正确结论(或结果):