题目内容
已知x，y都为正整数，且3| x |
| y |
| 3 |
分析：根据题意，得3
、
、10
是同类二次根式，即都含有
，可设3
=3m
，
=n
，得3m+n=10，再根据正整数确定m，n的值，从而求解．
| x |
| y |
| 3 |
| 3 |
| x |
| 3 |
| y |
| 3 |
解答：解：∵x、y都是正整数，
∴3
、
、10
是同类二次根式，
设3
=3m
，
=n
．
则3m+n=10，m、n是正整数，
∴
或
或
．
∵3
=3m
，
=n
．
∴3
=3
，
∴x=3，
∴
=7
．
∴y=147，
同理可得：
此时
或
或
．
∴3
| x |
| y |
| 3 |
设3
| x |
| 3 |
| y |
| 3 |
则3m+n=10，m、n是正整数，
∴
|
|
|
∵3
| x |
| 3 |
| y |
| 3 |
∴3
| x |
| 3 |
∴x=3，
∴
| y |
| 3 |
∴y=147，
同理可得：
此时
|
|
|
点评：此题考查了同类二次根式的定义和二元一次方程的正整数解的求解方法．
练习册系列答案
相关题目
（n为正整数，且0<a1<a2<…<an）与x轴的交点为An-1（bn-1,0）和An(bn，0)，当n=1时，第1条抛物线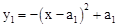
与x轴的交点为A0（0，0）和A1（b1，0），其他依此类推．
，求x，y的值．