Question

【题目】已知：如图，梯形ABCD与梯形A′B′C′D′相似，AD∥BC，A′D′∥B′C′，∠A＝∠A′．AD＝4，A′D′＝6，AB＝6，B′C′＝12．求：

(1)梯形ABCD与梯形A′B′C′D′的相似比k；

(2)A′B′和BC的长；

(3)D′C′∶DC．

Answer 1

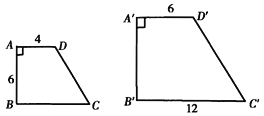
【答案】(1)k＝2∶3；(2)A＇B＇＝9，BC＝8；(3)3∶2．

【解析】

根据相似多边形的对应边成比例列式计算即可求出.

∵梯形ABCD∽梯形A′B′C′D′相似，

∴AD：A′D′=4:6=2:3;

（2）由（1）知AB: A′B′= AD：A′D′=2:3，

∵AB=6，

∴A′B′=9；

同理可得，BC＝8；

（3）∵梯形ABCD∽梯形A′B′C′D′相似，

∴D′C′∶DC= A′D′：AD=3:2.