题目内容
已知△ABC中AB=AC=20，BC=24，则△ABC的面积为________．
192
分析：作出三角形底边上的高AD，由等腰三角形的性质和勾股定理求得高的值后，由面积公式求解．
解答：
解：作AD⊥BC于点D，则BD=
BC=12，
在Rt△ABD中，AD=
=16，
∴S△ABC=BC•AD=×24×16=192．
点评：本题利用了等腰三角形的性质：底边上的高平分底边，勾股定理和三角形的面积求解．
分析：作出三角形底边上的高AD，由等腰三角形的性质和勾股定理求得高的值后，由面积公式求解．
解答：
解：作AD⊥BC于点D，则BD=BC=12，在Rt△ABD中，AD=
=16，∴S△ABC=
BC•AD=×24×16=192．点评：本题利用了等腰三角形的性质：底边上的高平分底边，勾股定理和三角形的面积求解．
练习册系列答案
阅读快车系列答案
相关题目
19、已知△ABC中AB=AC=10，DE垂直平分AB，交AC于E．已知△BEC的周长是16，求△ABC的周长．
（2013•嘉定区一模）如图已知△ABC中AB=AC=10，BC=16，矩形DEFG的边EF在△ABC的边BC上，顶点D、G分别在AB、AC上，设DE的长为x，矩形DEFG的面积为y，求y关于x的函数关系式，并写出这个函数的定义域．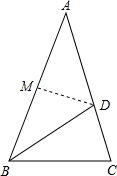
如图，已知△ABC中 AB=AC，∠A=36°，使点A、B重合对折，折痕为MD，连接BD．若△BCD的周长为5，BC=2．