题目内容
如图，点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，连接CD交OM于点N，则下列结论：①MC=MD，②∠CMO=∠DMO，③OM⊥CD，且NC=ND，④若∠1=30°，则OD=2MD，正确的有（ ）
| A．①②③ | B．①②④ | C．③④ | D．①③④ |
∵点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，
∴MC=MD，
∴△OMC≌△OMD，
∴∠CMO=∠DMO，
∴△ONC≌△OND，
∴∠ONC=∠OND=90°，
即OM⊥CD．
∴①②③对．
④应为若∠1=30°，则OM=2MD，故本选项错误．
故选A．
∴MC=MD，
∴△OMC≌△OMD，
∴∠CMO=∠DMO，
∴△ONC≌△OND，
∴∠ONC=∠OND=90°，
即OM⊥CD．
∴①②③对．
④应为若∠1=30°，则OM=2MD，故本选项错误．
故选A．
练习册系列答案
相关题目
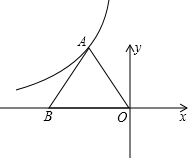
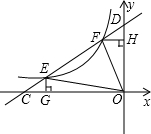
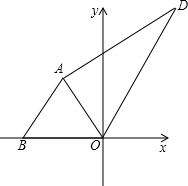
10、如图，点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，连接CD交OM于点N，则下列结论：①MC=MD，②∠CMO=∠DMO，③OM⊥CD，且NC=ND，④若∠1=30°，则OD=2MD，正确的有（ ）
如图，点M为∠COD的角平分线上一点，过点M作MC⊥OC于点C，MD⊥OD于点D，连接CD交OM于点N，则下列结论：①MC=MD，②∠CMO=∠DMO，③OM⊥CD，且NC=ND，④若∠1=30°，则OD=2MD，正确的有