题目内容
等边△ABO在直角坐标系中的位置如图所示,BO边在x轴上,点B的坐标为(-2,0)点,反比例函数y=| k |
| x |
(1)求这个反比例函数的解析式;
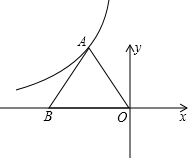
(2)如图,直线y=kx+2
| 3 |
| 7 |
| 8 |
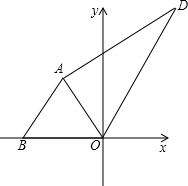
(3)如图,点D为(1)中的等边△ABO外任意一点,且∠ADO=30°,连接AD,OD,BD,则AD2,OD2,BD2之间存在一个数量关系,写出你的结论并加以证明.
分析:(1)根据等边三角形的性质和B点坐标求出A点坐标,然后用待定系数法求出解析式.
(2)根据面积关系和(1)的关系式可用带有k的式子表示出,又因为OD=2
,从而可确定出函数解析式.
(3)AD2,OD2,BD2之间存在的数量关系是BD2=OD2+AD2,以OD为边构造等边三角形ODP,连接AP,则△ADP为直角三角形;则AP2=DP2+AD2,可证△BOD≌△AOP(SAS),得BD=AP,从而可得BD2=DP2+AD2=OD2+AD2.
(2)根据面积关系和(1)的关系式可用带有k的式子表示出,又因为OD=2
| 3 |
(3)AD2,OD2,BD2之间存在的数量关系是BD2=OD2+AD2,以OD为边构造等边三角形ODP,连接AP,则△ADP为直角三角形;则AP2=DP2+AD2,可证△BOD≌△AOP(SAS),得BD=AP,从而可得BD2=DP2+AD2=OD2+AD2.
解答: 解:(1)则AB=BO=AO=2,过A作AM⊥BO于点M,
解:(1)则AB=BO=AO=2,过A作AM⊥BO于点M,
则OM=
BO=1,AM=
=
则点A的坐标为(-1,
)
则这个反比例函数的解析式为y=-
;
(2)∵S△DFH+S△FOE+S△ECG=
S△COD,
∴S△EGO+S△FOH=
S△COD
又∵S△EGO=S△FOH=
|k|=
,
则S△COD=8
,因为OD=2
,
∴OC=8,则C(-8,0),
∵直线y=kx+2
过C(-8,0),则k=
;
(3)AD2,OD2,BD2之间存在的数量关系是BD2=OD2+AD2,
以OD为边构造等边三角形ODP,连接AP,则△ADP为直角三角形;
则AP2=DP2+AD2
∵OB=OA,
∠BOD=∠AOP=60°+∠AOD,
OD=OP,
∴△BOD≌△AOP(SAS),
∴BD=AP
∴BD2=DP2+AD2=OD2+AD2.
 解:(1)则AB=BO=AO=2,过A作AM⊥BO于点M,
解:(1)则AB=BO=AO=2,过A作AM⊥BO于点M,则OM=
| 1 |
| 2 |
| AO2-OM2 |
| 3 |
则点A的坐标为(-1,
| 3 |
则这个反比例函数的解析式为y=-
| ||
| x |
(2)∵S△DFH+S△FOE+S△ECG=
| 7 |
| 8 |
∴S△EGO+S△FOH=
| 1 |
| 8 |
又∵S△EGO=S△FOH=
| 1 |
| 2 |
| ||
| 2 |
则S△COD=8
| 3 |
| 3 |
∴OC=8,则C(-8,0),
∵直线y=kx+2
| 3 |
| ||
| 4 |
(3)AD2,OD2,BD2之间存在的数量关系是BD2=OD2+AD2,

以OD为边构造等边三角形ODP,连接AP,则△ADP为直角三角形;
则AP2=DP2+AD2
∵OB=OA,
∠BOD=∠AOP=60°+∠AOD,
OD=OP,
∴△BOD≌△AOP(SAS),
∴BD=AP
∴BD2=DP2+AD2=OD2+AD2.
点评:本题考查的知识点比较多,属于难度比较大的题目,做的时候注意题目所给的条件,也要数形结合来做题.

练习册系列答案
相关题目
 12、等边△OAB在直角坐标系中的位置如图所示,折叠三角形使点B与y轴上的点C重合,折痕为MN,且CN平行于x轴,则∠CMN=
12、等边△OAB在直角坐标系中的位置如图所示,折叠三角形使点B与y轴上的点C重合,折痕为MN,且CN平行于x轴,则∠CMN= 如图,等边△ABC在直角坐标系xOy中,已知A(2,0),B(-2,0),点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
如图,等边△ABC在直角坐标系xOy中,已知A(2,0),B(-2,0),点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是 (x<0)经过点A.
(x<0)经过点A.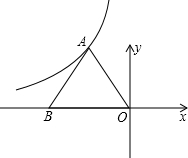
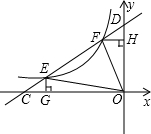
 与x轴,y轴交于C,D两点,与(1)中的反比例函数的图象交于E,F两点,EG⊥x轴于G点,FH⊥y轴于H点,若△DFH的面积记为S△DFH,已知S△DFH+S△FOE+S△ECG=
与x轴,y轴交于C,D两点,与(1)中的反比例函数的图象交于E,F两点,EG⊥x轴于G点,FH⊥y轴于H点,若△DFH的面积记为S△DFH,已知S△DFH+S△FOE+S△ECG= S△COD,求k的值;
S△COD,求k的值;

 ,
, ,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
