题目内容
6．
如图，在△ABC中，∠B=40°，EF∥AB，∠1=50°，CE=3，EF比CF大1，则EF的长为（ ）| A． | 5 | B． | 6 | C． | 3 | D． | 4 |
分析 由平行线的性质得出∠A=∠1=50°，得出∠C=90°，设CF=x，则EF=x+1，根据勾股定理得出方程，解方程求出x，即可得出EF的长．
解答 解：∵EF∥AB，
∴∠A=∠1=50°，
∴∠A+∠B=50°+40°=90°，
∴∠C=90°，
设CF=x，则EF=x+1，
根据勾股定理得：CE2+CF2=EF2，
即32+x2=（x+1）2，
解得：x=4，
∴EF=4+1=5，
故选：A．
点评 本题考查了平行线的性质、直角三角形的判定、勾股定理；熟练掌握平行线的性质，并能进行推理论证与计算是解决问题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
16．
如图所示，已知直线a∥b，c与a，b均相交，∠1=60°，则∠2为（ ）
如图所示，已知直线a∥b，c与a，b均相交，∠1=60°，则∠2为（ ）| A． | 60° | B． | 70° | C． | 120° | D． | 150° |
如图，线段AB=18cm，反向延长AB到C，使BC=2AC，D是AB上一点，且BD=$\frac{1}{6}$BC，若M为CD的中点，求AM的长．
18．下列各式成立的是（ ）
| A． | -80＞0.8 | B． | -2.93＜-2.94 | C． | -π＞-3.14 | D． | $-\frac{3}{4}$＜$-\frac{2}{3}$ |
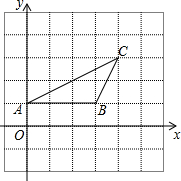如图，在平面直角坐标系中，若△ABC三点坐标分别为A（0，1），B（3，1），C（4，3），如果要找一点D，使△ABD与△ABC全等，那么点D的坐标是（4，-1）或（-1，3）或（-1，-1）．