题目内容
已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
求证:BC=DE.

考点:全等三角形的判定与性质。
专题:证明题。
分析:根据AC∥DE,证得∠ACD=∠D,∠BCA=∠E,通过等量代换可知∠B=∠D,再根据AC=CE,可证△ABC≌△CDE,所以BC=DE.
解答:证明:∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠E.
又∵∠ACD=∠B,
∴∠B=∠D.
在△ABC和△CDE中,

∴△ABC≌△CDE(AAS).
∴BC=DE.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:S![]() SS、SAS、SSA、HL.
SS、SAS、SSA、HL.![]() 判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为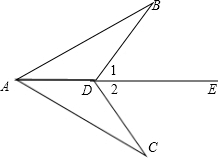 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为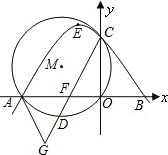 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧