题目内容
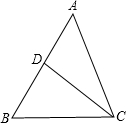 已知,D是△ABC的AB边上的一点,BD=
已知,D是△ABC的AB边上的一点,BD= ,AB=3,BC=2
,AB=3,BC=2
(1)△BCD与△BAC相似吗?说明理由.
(2)若△BCD的面积是4,求△ADC的面积.
解:(1)△BCD与△BAC相似.理由如下:
∵BD= ,AB=3,BC=2,
,AB=3,BC=2,
∴ =
= ,
, =
= ,
,
∴ =
= ,
,
而∠B=∠B,
∴△BCD∽△CBA;
(2)∵△BCD∽△CBA,
∴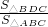 =(
=( )2=
)2= ,
,
而△BCD的面积是4,
∴S△ABC=9,
∴S△ADC=5.
分析:(1)△BCD与△BAC相似.由BD= ,AB=3,BC=2,得到
,AB=3,BC=2,得到 =
= ,
, =
= ,即
,即 =
= ,加上∠B公共,得到△BCD∽△CBA;
,加上∠B公共,得到△BCD∽△CBA;
(2)由△BCD∽△CBA,根据相似三角形面积的比等于相似比的平方得到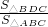 =(
=( )2=
)2= ,而△BCD的面积是4,得到S△ADC的值.
,而△BCD的面积是4,得到S△ADC的值.
点评:本题考查了三角形相似的判定与性质.有两组对应边的比相等,且它们的夹角相等的两个三角形相似.相似三角形面积的比等于相似比的平方.
∵BD=
 ,AB=3,BC=2,
,AB=3,BC=2,∴
 =
= ,
, =
= ,
,∴
 =
= ,
,而∠B=∠B,
∴△BCD∽△CBA;
(2)∵△BCD∽△CBA,
∴
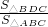 =(
=( )2=
)2= ,
,而△BCD的面积是4,
∴S△ABC=9,
∴S△ADC=5.
分析:(1)△BCD与△BAC相似.由BD=
 ,AB=3,BC=2,得到
,AB=3,BC=2,得到 =
= ,
, =
= ,即
,即 =
= ,加上∠B公共,得到△BCD∽△CBA;
,加上∠B公共,得到△BCD∽△CBA;(2)由△BCD∽△CBA,根据相似三角形面积的比等于相似比的平方得到
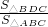 =(
=( )2=
)2= ,而△BCD的面积是4,得到S△ADC的值.
,而△BCD的面积是4,得到S△ADC的值.点评:本题考查了三角形相似的判定与性质.有两组对应边的比相等,且它们的夹角相等的两个三角形相似.相似三角形面积的比等于相似比的平方.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 (2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.
(2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC. 如图,已知点O是△ABC的∠ABC和∠ACB平分线的交点,过O作EF平行于BC交AB于E,交AC于F,AB=12,AC=18,则△AEF的周长是( )
如图,已知点O是△ABC的∠ABC和∠ACB平分线的交点,过O作EF平行于BC交AB于E,交AC于F,AB=12,AC=18,则△AEF的周长是( )