题目内容
如图，AC是圆的直径，∠B为直角，AB=6，BC=8，则阴影面积为
- A.100π-24
- B.25π-24
- C.100π-48
- D.25π-48
B
分析：首先根据勾股定求出AC的长，再根据阴影面积等于圆的面积-直角三角形的面积即可解答．
解答：∵AC是圆的直径，∠B为直角，AB=6，BC=8，∴AC=
=
=10，
∴S圆=π（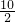
）2=25π，S△ABC=
AB•BC=×6×8=24，
∴S阴影=S圆-S△ABC=25π-24．
故选B．
点评：运用了勾股定理，熟悉圆面积公式和直角三角形的面积公式．
分析：首先根据勾股定求出AC的长，再根据阴影面积等于圆的面积-直角三角形的面积即可解答．
解答：∵AC是圆的直径，∠B为直角，AB=6，BC=8，∴AC=
==10，∴S圆=π（
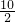）2=25π，S△ABC=AB•BC=×6×8=24，∴S阴影=S圆-S△ABC=25π-24．
故选B．
点评：运用了勾股定理，熟悉圆面积公式和直角三角形的面积公式．
练习册系列答案
相关题目
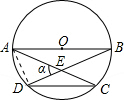如图，AB是圆的直径，CD是平行于AB的弦，且AC和BD相交于E，∠AED=α，那么△CDE与△ABE的面积之比是（ ）| A、cosα | B、sin2α | C、cos2α | D、1-sinα |
如图，AC是⊙O的直径，∠ACB=60°，连接AB，分别过A、B作圆O的切线，两切线交于点P，若已知⊙O的半径为1，求△PAB的周长．
如图，AC是圆的直径，∠B为直角，AB=6，BC=8，则阴影面积为（ ）| A、100π-24 | B、25π-24 | C、100π-48 | D、25π-48 |
