题目内容
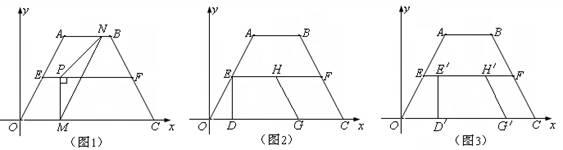
 如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为________.
如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为________.
 l
l分析:设AC=x,BC=l-x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=
 x,CD′=
x,CD′= (l-x),∵∠ACD=45°,∠BCD′=45°,∴∠DCD′=90°,根据勾股定理然后用配方法即可求解.
(l-x),∵∠ACD=45°,∠BCD′=45°,∴∠DCD′=90°,根据勾股定理然后用配方法即可求解.解答:设AC=x,BC=l-x,
∵△ABC,△BCD′均为等腰直角三角形,
∴CD=
 x,CD′=
x,CD′= (l-x),
(l-x),∵∠ACD=45°,∠BCD′=45°,
∴∠DCD′=90°,
∴DD′2=CD2+CD′2=
 x2+
x2+ (l-x)2
(l-x)2=x2-lx+
 l2=
l2= +
+ l2,
l2,∴当x取
 l时,DD′取最小值,最小值为:
l时,DD′取最小值,最小值为: l.
l.故答案为:
 l.
l.点评:本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目