题目内容
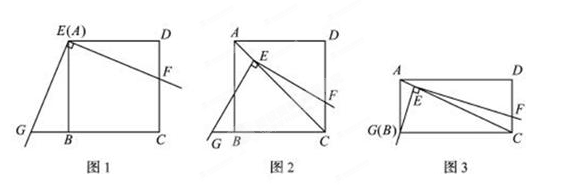
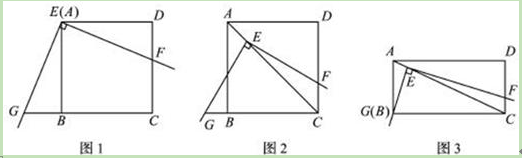
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,求![]() 的值.
的值.

图1 图2 图3
(1)证明:∵∠GEB+∠BEF=90°,∠DEF+∠BEF=90°,
∴∠DEF=GEB,………………………………………………( 1分)
又∵ED=BE,
∴Rt△FED≌Rt△GEB,…………………………………………( 2分)
∴EF=EG.……………………………………………………( 3分)
(2)成立.……………………………………………………………………( 4分)
证明:如图,过点E分别作BC、CD的垂线,垂足分别为H、I,
则EH=EI,∠HEI=90°,…………………………………( 5分)
![]() ∵∠GEH+∠HEF=90°,∠IEF+∠HEF=90°,
∵∠GEH+∠HEF=90°,∠IEF+∠HEF=90°,
∴∠IEF=∠GEH,……………………………………………( 6分)
∴Rt△FEI≌Rt△GEH,
∴EF=EG.………………………………………………………(7分)

(3)解:如图,过点E分别作BC、CD的垂线,垂足分别为M、N ,
则∠MEN=90°,EM∥AB,EN∥AD,………………………( 8分![]() )
)
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() , …………………………………………(9分)
, …………………………………………(9分)
∵∠GEM+∠MEF=90°,∠FEN+∠MEF=90°,
∴∠FEN=∠GEM,
∴Rt△FEN∽Rt△GEM, …………………………………………(10分)
∴![]() =
=![]() =
=![]() .…………………………………………(11分)
.…………………………………………(11分)

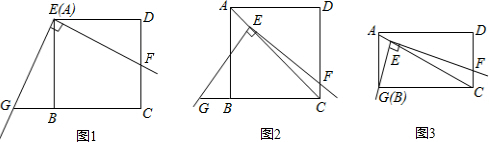
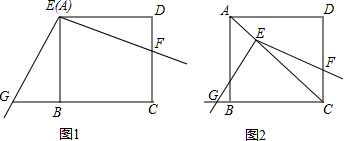
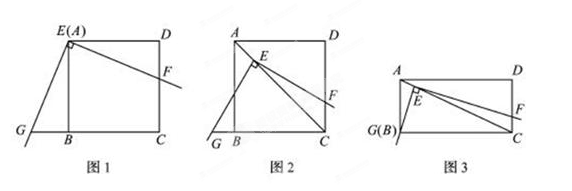
 将三角板放在正方形
将三角板放在正方形 上,使三角板的直角顶点
上,使三角板的直角顶点 与正方形
与正方形 重合,三角扳的一边交
重合,三角扳的一边交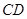 于点
于点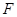 .另一边交
.另一边交 的延长线于点
的延长线于点 .
.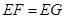 ;
;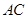 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理 由:
由: ,其他条件不变,若
,其他条件不变,若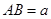 、
、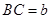 ,求
,求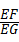 的值.
的值.