题目内容
解答题
(1)已知a、b、c均为实数,且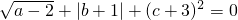 ,求方程ax2+bx+c=0的根.
,求方程ax2+bx+c=0的根.
(2)若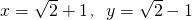 ,求
,求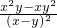 的值.
的值.
解:(1)∵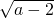 +|b+1|+(c+3)2=0,
+|b+1|+(c+3)2=0,
∴a=2,b=-1,c=-3,
∴方程为2x2-x-3=0,
分解因式,得(2x-3)(x+1)=0,
解得x1= ,x2=-1;
,x2=-1;
(2)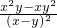 =
= =
= ,
,
当x= +1,y=
+1,y= -1时,原式=
-1时,原式= =
= .
.
分析:(1)根据非负数的性质求a、b、c的值,代入方程,利用“十字相乘法”解方程;
(2)先将分式化简,再代值计算.
点评:本题考查了因式分解法解一元二次方程,二次根式的化简求值.关键是根据方程的特点,运用十字相乘法解方程,在进行二次根式化简求值时,应先化简,再代值.
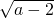 +|b+1|+(c+3)2=0,
+|b+1|+(c+3)2=0,∴a=2,b=-1,c=-3,
∴方程为2x2-x-3=0,
分解因式,得(2x-3)(x+1)=0,
解得x1=
 ,x2=-1;
,x2=-1;(2)
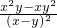 =
= =
= ,
,当x=
 +1,y=
+1,y= -1时,原式=
-1时,原式= =
= .
.分析:(1)根据非负数的性质求a、b、c的值,代入方程,利用“十字相乘法”解方程;
(2)先将分式化简,再代值计算.
点评:本题考查了因式分解法解一元二次方程,二次根式的化简求值.关键是根据方程的特点,运用十字相乘法解方程,在进行二次根式化简求值时,应先化简,再代值.

练习册系列答案
相关题目