题目内容
 如图,△ABC为正三角形,面积为S.D1,E1,F1分别是△ABC三边上的点,且AD1=BE1=CF1=
如图,△ABC为正三角形,面积为S.D1,E1,F1分别是△ABC三边上的点,且AD1=BE1=CF1= AB,可得△D1E1F1,则△D1E1F1的面积S1=________;如,D2,E2,F2分别是△ABC三边上的点,且AD2=BE2=CF2=
AB,可得△D1E1F1,则△D1E1F1的面积S1=________;如,D2,E2,F2分别是△ABC三边上的点,且AD2=BE2=CF2= AB,则△D2E2F2的面积S2=________;按照这样的思路探索下去,Dn,En,Fn分别是△ABC三边上的点,且
AB,则△D2E2F2的面积S2=________;按照这样的思路探索下去,Dn,En,Fn分别是△ABC三边上的点,且
ADn=BEn=CFn= AB,则Sn=________.
AB,则Sn=________.
 S
S  S
S 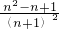 S
S分析:先利用边角边证明△AD1F1、△BD1E1、△CE1F1全等,再利用正弦定理的方法表示出△ABC的面积与△AD1F1的面积,然后根据△D1E1F1的面积等于△ABC的面积减去△AD1F1的面积的3倍列式进行计算即可;
先证明四周的三个三角形全等,然后用S表示出△AD2F2的面积,然后与第一问同理求解即可;
根据规律写出即可.
解答:∵△ABC为正三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵AD1=BE1=CF1=
 AB,
AB,∴BD1=CE1=AF1=
 AB,
AB,∴△AD1F1≌△BD1E1≌△CE1F1,
设等边△ABC的边长为a,
则S=
 a2sin60°,
a2sin60°,△AD1F1的面积=
 ×
× a•
a• a•sin60°=
a•sin60°= S,
S,∴△D1E1F1的面积S1=S-3×
 S=
S= S;
S;同理,AD2=BE2=CF2=
 AB时,
AB时,BD2=CE2=AF2=
 AB,
AB,△AD2F2的面积S2=
 ×
× a•
a• a•sin60°=
a•sin60°= S,
S,△D2E2F2的面积S2=S-3×
 S=
S= S;
S;ADn=BEn=CFn=
 AB时,
AB时,BDn=CEn=AFn=
 AB,
AB,△ADnFn的面积=
 ×
× a•
a• a•sin60°=
a•sin60°= S,
S,△DnEnFn的面积Sn=S-3×
 S=
S=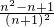 S.
S.故答案为:
 S,
S, S,
S,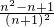 S.
S.点评:本题考查了等边三角形的性质,全等三角形的判定,利用正弦定理的方法表示出三角形的面积是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,△ABC中,AB=BC=CA=8.一电子跳蚤开始时在BC边的P0处,BP0=3.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( )
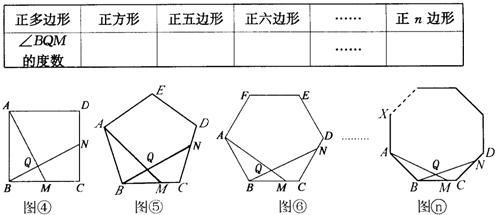
如图,△ABC中,AB=BC=CA=8.一电子跳蚤开始时在BC边的P0处,BP0=3.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( )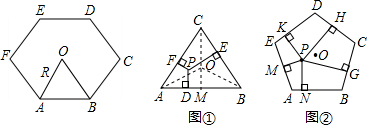 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
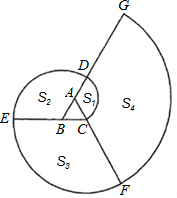 依次为A、B、C….当渐开线延伸开时,形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1.
依次为A、B、C….当渐开线延伸开时,形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1. 如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3
如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2