题目内容
如图,抛物线y=ax2+bx+c经过原点O,与x轴交于另一点N,直线y=kx+4与两坐标轴分别交于A、D两点,与抛物线交于点B(1,m)、C(2,2).
【小题1】求直线与抛物线的解析式.
【小题2】若抛物线在x轴上方的部分有一动点P(x,y),设∠PON=
 ,求当△PON的面积最大时tan
,求当△PON的面积最大时tan 的值.
的值.【小题3】若动点P保持(2)中的运动线路,问是否存在点P,使得△POA的面积等于△PON的面积的?若存在,请求出点P的坐标;若不存在,请说明理由
p;【答案】
【小题1】将点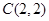 代入直线
代入直线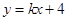 可得
可得
所以直线的解析式为 …………………………………………2分
…………………………………………2分
当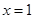 时,
时,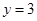 ,所以
,所以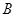 点的坐标为(1,3),
点的坐标为(1,3),
将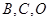 三点的坐标分别代入抛物线
三点的坐标分别代入抛物线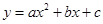 ,可得
,可得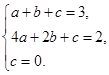
解得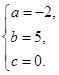 所以所求的抛物线为
所以所求的抛物线为 .…………………….5分
.…………………….5分
【小题2】∵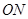 的长是定值,∴当点
的长是定值,∴当点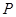 为抛物线的顶点时,
为抛物线的顶点时,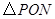 的面积最大.
的面积最大.
由 =
= 得,该抛物线的顶点坐标为
得,该抛物线的顶点坐标为 ,此时
,此时 .………………………………………………….8分
.………………………………………………….8分
【小题3】存在……………………………………………………………………9分
把 代入
代入 得
得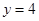 ,∴点
,∴点
把 代入
代入 得
得 或
或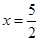 ,∴点
,∴点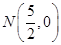 .
.
∴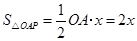 ,
,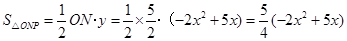
由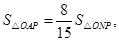 即
即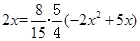
解得 (舍去)或
(舍去)或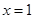 , 当
, 当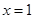 时,
时,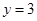
∴存在点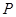 ,其坐标为(1,3).…………………………………………….12分解析:
,其坐标为(1,3).…………………………………………….12分解析:
略
【小题1】将点
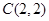 代入直线
代入直线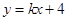 可得
可得
所以直线的解析式为
 …………………………………………2分
…………………………………………2分当
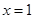 时,
时,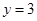 ,所以
,所以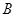 点的坐标为(1,3),
点的坐标为(1,3),将
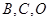 三点的坐标分别代入抛物线
三点的坐标分别代入抛物线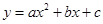 ,可得
,可得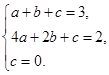
解得
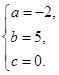 所以所求的抛物线为
所以所求的抛物线为 .…………………….5分
.…………………….5分【小题2】∵
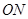 的长是定值,∴当点
的长是定值,∴当点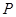 为抛物线的顶点时,
为抛物线的顶点时,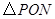 的面积最大.
的面积最大.由
 =
= 得,该抛物线的顶点坐标为
得,该抛物线的顶点坐标为 ,此时
,此时 .………………………………………………….8分
.………………………………………………….8分【小题3】存在……………………………………………………………………9分
把
 代入
代入 得
得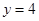 ,∴点
,∴点
把
 代入
代入 得
得 或
或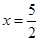 ,∴点
,∴点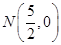 .
.∴
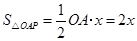 ,
,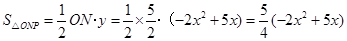
由
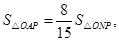 即
即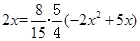
解得
 (舍去)或
(舍去)或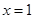 , 当
, 当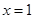 时,
时,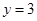
∴存在点
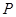 ,其坐标为(1,3).…………………………………………….12分解析:
,其坐标为(1,3).…………………………………………….12分解析:略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




