题目内容
5.对某一种四边形给出如下定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.则∠C=130度,∠D=80度.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形ABCD”(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②在①的条件下,若∠ABC=∠ADC=90°,AB=AD=4,∠BCD=60°,求等对角四边形ABCD的面积.

分析 (1)根据四边形ABCD是“等对角四边形”得出∠D=∠B=80°,根据多边形内角和定理求出∠C即可;
(2)①连接BD,根据等边对等角得出∠ABD=∠ADB,求出∠CBD=∠CDB,根据等腰三角形的判定得出即可;
②连接AC,求出△ABC≌△ADC,求出∠ACB=∠ACD=30°,解直角三角形求出AC和BC,根据三角形的面积公式求出即可.
解答 解:(1)∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°,
∴∠D=∠B=80°,
∴∠C=360°-80°-80°-70°=130°,
故答案为:130,80;
(2)①证明:如图1,连接BD,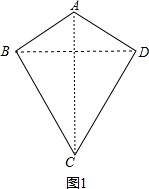
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC-∠ABD=∠ADC-∠ADB.
∴∠CBD=∠CDB,
∴CB=CD;
②解:如图1,连接AC,
∵在△ABC和△ADC中
$\left\{\begin{array}{l}{AB=AD}\\{∠ABC=∠ADC}\\{CB=CD}\end{array}\right.$,
∴△ABC≌△ADC
∴∠ACB=∠ACD=$\frac{1}{2}$∠BCD=$\frac{1}{2}$×60°=30°,
∵在Rt△ABC中,∠ACB=30°,AB=AD=4,
∴AC=2AB=8,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴S四边形ABCD=2S△ABC=2×$\frac{1}{2}$×4×4$\sqrt{3}$=16$\sqrt{3}$.
点评 本题考查了含30°角的直角三角形性质,勾股定理,全等三角形的性质和判定的应用,能综合运用性质进行推理和计算是解此题的关键,综合性比较强,难度偏大.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案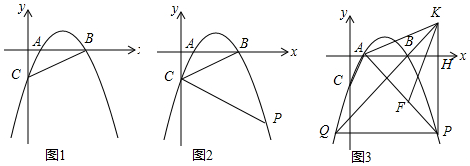

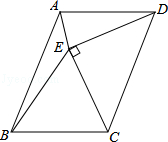 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是135°.
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是135°.