题目内容
17.若关于x的一元二次方程(a-1)x2-2x+2=0有实数根,则整数a的最大值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 由关于x的一元二次方程(a-1)x2-2x+2=0有实数根,则a-1≠0,且△≥0,即△=(-2)2-8(a-1)=12-8a≥0,解不等式得到a的取值范围,最后确定a的最大整数值.
解答 解:∵关于x的一元二次方程(a-1)x2-2x+2=0有实数根,
∴△=(-2)2-8(a-1)=12-8a≥0且a-1≠0,
∴a≤$\frac{3}{2}$且a≠1,
∴整数a的最大值为0.
故选:B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义和不等式的特殊解.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
7.下列计算正确的是( )
| A. | 2a•3b=5ab | B. | a3•a4=a12 | C. | (-3a2b)2=6a4b2 | D. | a5÷a3+a2=2a2 |
6.下列运算正确的是( )
| A. | 5m+2m=7m2 | B. | -2m2•m3=2m5 | C. | (-a2b)3=-a6b3 | D. | (b+2a)(2a-b)=b2-4a2 |
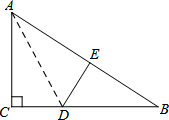 如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.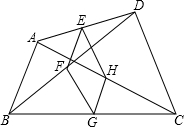 如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?
如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?