题目内容
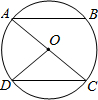
 已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为
已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为考点:圆周角定理
专题:
分析:首先根据垂直定义可得∠O=90°,再根据圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半可得答案.
解答:解:∵OA⊥OB,
∴∠O=90°,
∴∠ACB=90°×
=45°,
故答案为:45°.
∴∠O=90°,
∴∠ACB=90°×
| 1 |
| 2 |
故答案为:45°.
点评:此题主要考查了圆周角定理,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
 如图,AC是⊙O的直径,AB,CD是⊙O的两条弦,且AB∥CD.如果∠BAC=32°,则∠AOD的度数是( )
如图,AC是⊙O的直径,AB,CD是⊙O的两条弦,且AB∥CD.如果∠BAC=32°,则∠AOD的度数是( )| A、16° | B、32° |
| C、48° | D、64° |