题目内容
 如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数y1=
如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数y1=| m |
| x |
(1)求m,n的值;
(2)设直线AB的函数解析式为y2=kx+b(b≠0),请求出这条直线的解析式;
(3)求△OCD的面积;
(4)直接写出当y1>y2时,自变量x的取值范围.
考点:反比例函数综合题
专题:
分析:(1)将点C(1,6)代入y=
,求出m的值,再根据函数解析式求出n的值;
(2)根据C、D的坐标,利用待定系数法求出一次函数解析式;
(3)根据S△DOC=S△AOB-S△AOC-S△BOD即可得到△OCD的面积;
(4)根据两个图象的位置可知当y1>y2时y1的图象位于y2的图象的上方,从而求解;
| m |
| x |
(2)根据C、D的坐标,利用待定系数法求出一次函数解析式;
(3)根据S△DOC=S△AOB-S△AOC-S△BOD即可得到△OCD的面积;
(4)根据两个图象的位置可知当y1>y2时y1的图象位于y2的图象的上方,从而求解;
解答:解:(1)将C(1,6)代入,m=1×6=6,则函数解析式为y=,
将D(3,n)代入y=
得,n=
=2,
故m=6,n=2.
(2)设AB的解析式为y=kx+b,
将C(1,6)、D(3,2)分别代入解析式得,
,
解得
,
则函数解析式为y=-2x+8.
(3)如图:作DG⊥y轴,垂足为G,
∵C(1,6),D(3,2),
∴CE=1,DF=2,
令x=0,代入y=-2x+8,得y=8,
∴A(0,8),
令y=0,代入y=-2x+8,得x=4,
∴B(4,0),
∴OA=8,OB=4,
∴S△DOC=S△AOB-S△AOC-S△BOD
=
×OA×OB-
×OA×CE-
×OB×DF
=
×8×4-
×8×1-
×4×2
=8;
(4)观察图象得:当y1>y2时,自变量x的取值范围为:0<x<1或x>3;
将D(3,n)代入y=
| 6 |
| x |
| 6 |
| 3 |
故m=6,n=2.
(2)设AB的解析式为y=kx+b,
将C(1,6)、D(3,2)分别代入解析式得,
|
解得
|
则函数解析式为y=-2x+8.
(3)如图:作DG⊥y轴,垂足为G,
∵C(1,6),D(3,2),
∴CE=1,DF=2,
令x=0,代入y=-2x+8,得y=8,
∴A(0,8),
令y=0,代入y=-2x+8,得x=4,
∴B(4,0),
∴OA=8,OB=4,
∴S△DOC=S△AOB-S△AOC-S△BOD
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=8;
(4)观察图象得:当y1>y2时,自变量x的取值范围为:0<x<1或x>3;
点评:本题考查了用待定系数法求一次函数和反比例函数的解析式,三角形面积,一次函数与反比例函数的交点问题的应用,关键是求出两函数的解析式.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
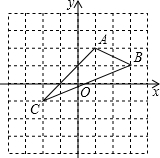 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).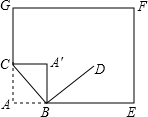 如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数.
如图,将书页一角斜折过去,使角的顶点A落在A′处,BC为折痕,BD平分∠A′BE,求∠CBD的度数. 在矩形ABCD中,点E,F在边DC上,EF=10米,点G在AB上,AG=52米,若∠EAB=36°,∠FGB=72°,求BC的长(精确到个位).
在矩形ABCD中,点E,F在边DC上,EF=10米,点G在AB上,AG=52米,若∠EAB=36°,∠FGB=72°,求BC的长(精确到个位).