题目内容
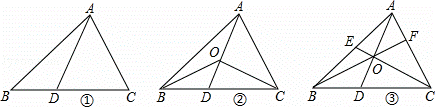
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想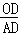 +
+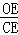 +
+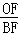 的值,并说明理由.
的值,并说明理由.
解:(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=1:2;当点D是BC边上任意一点时,S△ABD:S△ABC=BD:BC,
故答案为:1:2,BD:BC;
(2)S△BOC:S△ABC=OD:AD,
如图②作OE⊥BC与E,作AF⊥BC与F,,
∵OE∥AF,
∴△OED∽△AFD,
 .
.
∵ ,
,
∴ ;
;
(3) +
+ +
+ =1,理由如下:
=1,理由如下:
由(2)得 ,
, ,
, .
.
∴ +
+ +
+ =
=
=
=
=1.


不等式组 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
|
| A. |
| B. |
| C. |
| D. |
|
如图,∠BAC=40°,DE∥AB,交AC于点F,∠AFE的平分线 FG交AB于点H,则正确的是( )
A.∠AFG=70° B.∠AFG>∠AHF
C.∠FHB=100° D.∠CFH =2∠EFG
 |
某公司为了开发新产品,用A、B两种原料各360千克、290千克,试制甲、乙两种新型产品共50件,下表是试验每件新产品所需原料的相关数据:
|
| A(单位:千克) | B(单位:千克) |
| 甲 | 9 | 3 |
| 乙 | 4 | 10 |
(1)设生产甲种产品x件,根据题意列出不等式组,求出x 的取值范围;(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,求出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各
的取值范围;(2)若甲种产品每件成本为70元,乙种产品每件成本为90元,设两种产品的成本总额为y元,求出成本总额y(元)与甲种产品件数x(件)之间的函数关系式;当甲、乙两种产品各 生产多少件时,产品的成本总额最少?并求出最少的成本总额.
生产多少件时,产品的成本总额最少?并求出最少的成本总额.





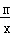 (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
 是一个完全平方式,那么
是一个完全平方式,那么 的值为 .
的值为 .
