题目内容
△ABC是等腰直角三角形，如图，AB=AC，∠BAC=90°，D是BC上一点，△ACD经过旋转到达△ABE的位置，则其旋转角的度数为________．
90°
分析：根据题意可得AB与AC是旋转前后的对应边，根据旋转变换的性质，∠BAC的度数即为旋转角的度数，从而得解．
解答：∵△ACD经过旋转到达△ABE的位置，
∴点A为旋转中心，AB与AC是对应边，
∴∠BAC即为旋转角，
∵∠BAC=90°，
∴旋转角的度数为90°．
故答案为：90°．
点评：本题主要考查了等腰直角三角形的性质，旋转变换的性质，结合图形找出旋转中心与对应边是解题的关键．
分析：根据题意可得AB与AC是旋转前后的对应边，根据旋转变换的性质，∠BAC的度数即为旋转角的度数，从而得解．
解答：∵△ACD经过旋转到达△ABE的位置，
∴点A为旋转中心，AB与AC是对应边，
∴∠BAC即为旋转角，
∵∠BAC=90°，
∴旋转角的度数为90°．
故答案为：90°．
点评：本题主要考查了等腰直角三角形的性质，旋转变换的性质，结合图形找出旋转中心与对应边是解题的关键．
练习册系列答案
相关题目
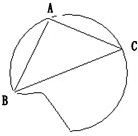如图，要把破残的圆形模具复制完整，已知弧上的三点A、B、C；
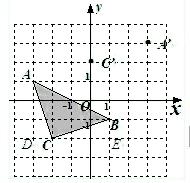16、如图，在画有方格图的平面直角坐标系中，△ABC的三个顶点均在格点上．
在△ABC中，∠ACB=90°，点A的坐标为（0，2），点B（-3，1）在抛物线y=ax2+ax-2上，点C在x轴上．