题目内容
 如图,⊙O的直径CD⊥弦AB于点P,且点P为OD的中点,已知AB=2
如图,⊙O的直径CD⊥弦AB于点P,且点P为OD的中点,已知AB=2 ,则CD的值为
,则CD的值为
- A.2
- B.4
- C.
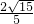
- D.
B
分析:连接OA,由CD垂直于AB,利用垂径定理得到P为AB的中点,求出AP的长,设OA=OD=x,由P为OD中点,得到OP为 x,在直角三角形AOP中,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,即为圆的半径,进而求出CD的长.
x,在直角三角形AOP中,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,即为圆的半径,进而求出CD的长.
解答: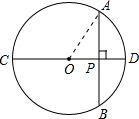 解:连接OA,
解:连接OA,
∵CD⊥AB,
∴P为AB的中点,
∴AP= AB=
AB= ,
,
∵P为AB的中点,
∴OP=PD= OD,
OD,
在Rt△AOP中,OA=x,OP= x,
x,
根据勾股定理得:OA2=OP2+AP2,
即x2= x2+3,即x2=4,
x2+3,即x2=4,
解得:x=2,
则CD=4.
故选B
点评:此题考查了垂径定理,勾股定理,利用了方程的思想,熟练掌握垂径定理是解本题的关键.
分析:连接OA,由CD垂直于AB,利用垂径定理得到P为AB的中点,求出AP的长,设OA=OD=x,由P为OD中点,得到OP为
 x,在直角三角形AOP中,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,即为圆的半径,进而求出CD的长.
x,在直角三角形AOP中,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,即为圆的半径,进而求出CD的长.解答:
 解:连接OA,
解:连接OA,∵CD⊥AB,
∴P为AB的中点,
∴AP=
 AB=
AB= ,
,∵P为AB的中点,
∴OP=PD=
 OD,
OD,在Rt△AOP中,OA=x,OP=
 x,
x,根据勾股定理得:OA2=OP2+AP2,
即x2=
 x2+3,即x2=4,
x2+3,即x2=4,解得:x=2,
则CD=4.
故选B
点评:此题考查了垂径定理,勾股定理,利用了方程的思想,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )
如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )| A、80° | B、50° | C、40° | D、20° |
 如图,⊙O的直径CD过弦EF的中点G,∠OEF=34°,则∠DCF的度数是
如图,⊙O的直径CD过弦EF的中点G,∠OEF=34°,则∠DCF的度数是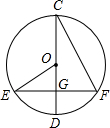 如图,⊙O的直径CD过弦EF的中点G,∠EOG=60°,则∠DCF的度数为
如图,⊙O的直径CD过弦EF的中点G,∠EOG=60°,则∠DCF的度数为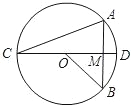 如图,⊙O的直径CD过弦AB的中点M,∠ACD=28°,则∠B=
如图,⊙O的直径CD过弦AB的中点M,∠ACD=28°,则∠B=