Question

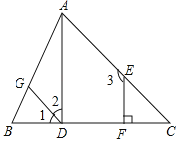
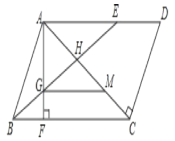
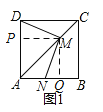
【题目】如图1，点M放在正方形ABCD的对角线AC(不与点A重合)上滑动，连结DM，做MN⊥DM,交直线AB于N．

(1)求证：DM=MN；

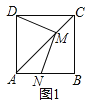
(2)若将(1)中的正方形变为矩形，其余条件不变如图，且DC=2AD，求MD:MN的值；

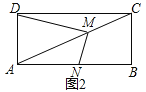
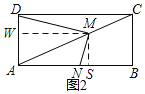
(3)在(2)中，若CD=nAD，当M滑动到CA的延长线上时(如图3)，请你直接写出MD：MN的比值．

Answer 1

【答案】见解析

【解析】分析：（1）过M作MQ⊥AB于Q，MP⊥AD于P，则∠PMQ=90°，∠MQN=∠MPD=90°，根据ASA即可判定△MDP≌△MNQ，进而根据全等三角形的性质得出DM=MN；
（2）过M作MS⊥AB于S，MW⊥AD于W，则∠WMS=90°，根据∠DMW=∠NMS，∠MSN=∠MWD=90°，判定△MDW∽MNS，得出MD：MN=MW：MS=MW：WA，再根据△AWM∽△ADC，DC=2AD，即可得出MD：MN=MW：WA=CD：DA=2；
（3）过M作MX⊥AB于X，MR⊥AD于R，则易得△NMX∽△DMR，得出MD：MN=MR：MX=AX：MX，再由AD∥MX，CD∥AX，易得△AMX∽△CAD，得出AX：MX=CD：AD，最后根据CD=nAD，即可得出MD：MN=CD：AD=n．

详解：

证明：过M作于于P，则，

，

，

是正方形，

平分，

，

在和中，

，

≌，

；

过M作于于W，则，

，

，

又，

∽MNS，

：：：WA，

，

，

∽，

又，

：：：；

：，

理由：过M作于于R，

则易得∽，

：：：MX，

由，易得∽，

：：AD，

又，

：：．