题目内容
如果矩形ABCD的对角线的交点与平面直角坐标系的原点重合,且点A和点B的坐标分别为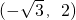 和
和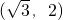 .矩形的面积为
.矩形的面积为
- A.

- B.

- C.

- D.
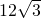
C
分析:根据已知和矩形的性质求出AB和BC的长,根据矩形的面积等于AB•BC,代入求出即可.
解答:∵矩形ABCD的对角线的交点与平面直角坐标系的原点重合,且点A和点B的坐标分别为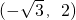 和
和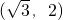 ,
,
∴AB= +
+ =2
=2 ,
,
BC=2+2=4,
∴矩形的面积是AB•BC=2 ×4=8
×4=8 ,
,
故选C.
点评:本题主要考查对矩形的性质,坐标与图形性质等知识点的理解和掌握,能根据已知求出AB和BC的长是解此题的关键.
分析:根据已知和矩形的性质求出AB和BC的长,根据矩形的面积等于AB•BC,代入求出即可.
解答:∵矩形ABCD的对角线的交点与平面直角坐标系的原点重合,且点A和点B的坐标分别为
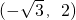 和
和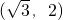 ,
,∴AB=
 +
+ =2
=2 ,
,BC=2+2=4,
∴矩形的面积是AB•BC=2
 ×4=8
×4=8 ,
,故选C.
点评:本题主要考查对矩形的性质,坐标与图形性质等知识点的理解和掌握,能根据已知求出AB和BC的长是解此题的关键.

练习册系列答案
相关题目
(1)如图①,P为△ABC的边AB上一点(P不与点A、点B重合),连接PC,如果△CBP∽△ABC,那么就称P为△ABC的边AB上的相似点.
画法初探
①如图②,在△ABC中,∠ACB>90°,画出△ABC的边AB上的相似点P(画图工具不限,保留画图痕迹或有必要的说明);
 |
辩证思考
②是不是所有的三角形都存在它的边上的相似点?如果是,请说明理由;如果不是,请找出一个不存在边上相似点的三角形;
特例分析
③已知P为△ABC的边AB上的相似点,连接PC,若△ACP∽△ABC,则△ABC的形状是 ▲ ;
④如图③,在△ABC中,AB=AC,∠A=36°,P是边AB上的相似点,求![]() 的值.
的值.
(2)在矩形ABCD中,AB=a,BC=b(a≥b).P是AB上的点(P不与点A、点B重合),作PQ⊥CD,垂足为Q.如果矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.
 ①类比(1)中的“画法初探”,可以提出问题:对于如图④的矩形ABCD,在不限制画图工具的前提下,如何画出它的边AB、CD上的相似线PQ呢?
①类比(1)中的“画法初探”,可以提出问题:对于如图④的矩形ABCD,在不限制画图工具的前提下,如何画出它的边AB、CD上的相似线PQ呢?
你的解答是: ▲ (只需描述PQ的画法,不需在图上画出PQ).
②请继续类比(1)中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究,要求每个栏目提出一个问题并解决.
 m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).
m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).



