题目内容
在平面直角坐标系xOy中,一次函数y=- x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
x+3的图象与x轴交于点A,与y轴交于点B,动点P从点B出发沿BA向终点A运动,同时动点Q从点O出发沿OB向点B运动,到达点B后立刻以原来的速度沿BO返回.点P,Q运动速度均为每秒1个单位长度,当点P到达点A时停止运动,点Q也同时停止.连结PQ,设运动时间为t(t>0)秒.
(1)求点P的坐标(用含t的代数式表示);
(2)当点Q从点O向点B运动时(未到达点B),是否存在实数t,使得△BPQ的面积大于17若存在,请求出t的取值范围;若不存在,请说明理由;
(3)伴随着P,Q两点的运动,线段PQ的垂直平分线为直线l.是否存在t的值,使得直线l经过点O?若存在,请求出所有t的值;若不存在,请说明理由.
(1)P(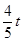 ,﹣
,﹣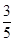 x+3);
x+3);
(2)不存在实数t,使得△BPQ的面积大于17;
(3),t=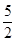 或
或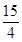 时,O在l的垂直平分线上.
时,O在l的垂直平分线上.
解析试题分析:(1)表示边长首要就是表示出来,根据函数性质及线段成比例等性质易表示出,PD,PC的长,即得坐标;
(2)讨论面积一般是计算底和高,然后表示出面积解析式,进而根据二次函数性质讨论最值或范围.而第一问求得OA=3,OB=4,易得S△AOB仅为6,而S△BQP≤S△AOB,所以定不存在实数t,使得面积大于17;
(3)垂直平分线上的点到两边距离相等,利用这个性质,我们只要表示出OP,和OQ即可.但讨论时注意Q点的运动时个往返的过程,要有两种情形.
试题解析:(1)如图,过点P作PC⊥OA于C,PD⊥OB于D.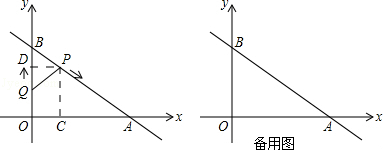
∵y=﹣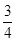 x+3的图象与x轴交于点A,与y轴交于点B
x+3的图象与x轴交于点A,与y轴交于点B
∴A(4,0),B(0,3),
在Rt△BDP中,
∵OB=3,OA=4,
∴AB=5.
∵BP∥OA,
∴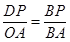 ,
,
∵BP=t,
∴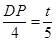 ,
,
∴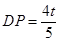 .
.
∵由点P过AB,
∴将x=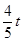 代入y=﹣
代入y=﹣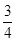 x+3,得y=﹣
x+3,得y=﹣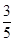 x+3,
x+3,
∴P(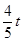 ,﹣
,﹣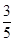 x+3);
x+3);
(2)不存在实数t,使得△BPQ的面积大于17.
∵Q、P在OB、OA上运动,
∴S△BQP≤S△AOB.
∵S△AOB= OA·OB=
OA·OB=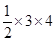 =6,
=6,
∴S△BQP≤6<17,
∴不存在实数t,使得△BPQ的面积大于17;
(3)∵P(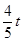 ,﹣
,﹣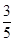 x+3),
x+3),
∴OC=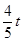 ,PC=﹣
,PC=﹣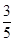 x+3,
x+3,
∴OP2=(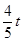 )2+(﹣
)2+(﹣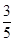 x+3)2,
x+3)2,
∵O在l的垂直平分线上,
∴OP=OQ.
①当0<t≤3时,OP=t,则t2=(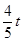 )2+(﹣
)2+(﹣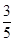 t+3)2,解得 t=
t+3)2,解得 t=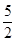 ,符合要求.
,符合要求.
②当3<t≤5时,
∵BQ=t﹣3,
∴OQ=3﹣(t﹣3)=6﹣t,
∴(6﹣t)2=(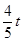 )2+(﹣
)2+(﹣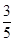 t+3)2
t+3)2
解得 t=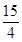 ,符合要求.
,符合要求.
综上所述,t=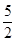 或
或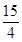 时,O在l的垂直平分线上.
时,O在l的垂直平分线上.
考点:一次函数综合题.

温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)当n=200时,
①根据信息填表:
| | A地 | B地 | C地 | 合计 |
| 产品件数(件) | x | | 2x | 200 |
| 运费(元) | 30x | | | |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.

 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
 的两根.
的两根.
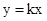 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标; ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;

