题目内容
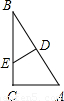
 如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是
如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是
- A.80°
- B.90°
- C.100°
- D.135°
B
分析:根据两直线平行,内错角相等可得∠1=∠2,然后根据翻折变换的性质以及三角形内角和定理列出方程组求解即可.
解答: 解:如图,∵DE∥AB,
解:如图,∵DE∥AB,
∴∠1=∠2,
∵△ABC沿DE折叠顶点C落在边AB上,
∴ ,
,
解得 .
.
故选B.
点评:本题考查了平行线的性质,翻折变换的性质,三角形内角和定理,熟记性质与定理并列出方程组是解题的关键.
分析:根据两直线平行,内错角相等可得∠1=∠2,然后根据翻折变换的性质以及三角形内角和定理列出方程组求解即可.
解答:
 解:如图,∵DE∥AB,
解:如图,∵DE∥AB,∴∠1=∠2,
∵△ABC沿DE折叠顶点C落在边AB上,
∴
 ,
,解得
 .
.故选B.
点评:本题考查了平行线的性质,翻折变换的性质,三角形内角和定理,熟记性质与定理并列出方程组是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,一张三角形纸片沿DE对折,点B与点A重合,若AB=
如图,一张三角形纸片沿DE对折,点B与点A重合,若AB= 如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是( )
如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是( )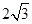 ,∠B=30°,则折痕DE的长为 .
,∠B=30°,则折痕DE的长为 . 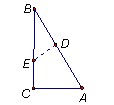
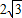 ,∠B=30°,则折痕DE的长为 .
,∠B=30°,则折痕DE的长为 .
 ,∠B=30°,则折痕DE的长为 .
,∠B=30°,则折痕DE的长为 .