题目内容
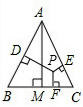
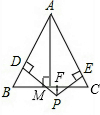
设点P在等边三角形ABC的外接圆的劣弧BC上(与B、C点不重合),则判断PA与PB+PC的大小关系:PA________PB+PC.
=
分析:在PA上截取PE=PC,连接CE,由圆周角定理可求出∠APC=60°,△PCE是等边三角形,PC=PE,由PC=PE,∠PCE=∠ACB=60°及圆周角定理可求出△ACE≌△PBC,即PB=AE,进而可求出结论.
解答: 解:在PA上截取PE=PC,连接CE,
解:在PA上截取PE=PC,连接CE,
∵△ABC是等边三角形,
∴∠APC=∠ABC=60°,
∴△PCE是等边三角形,
∴PC=CE,∠PCE=∠ACB=60°,
∴∠PCB=∠ACE,
∵BC=AC,∠PBC=∠CAE,
∴△ACE≌△PBC,
∴PB=AE,
∴PA=PB+PC.
点评:此题比较复杂,解答此题的关键是在PA上截取PE=PC,构造出等边三角形,再利用全等三角形的判定定理及性质解答即可.
分析:在PA上截取PE=PC,连接CE,由圆周角定理可求出∠APC=60°,△PCE是等边三角形,PC=PE,由PC=PE,∠PCE=∠ACB=60°及圆周角定理可求出△ACE≌△PBC,即PB=AE,进而可求出结论.
解答:
 解:在PA上截取PE=PC,连接CE,
解:在PA上截取PE=PC,连接CE,∵△ABC是等边三角形,
∴∠APC=∠ABC=60°,
∴△PCE是等边三角形,
∴PC=CE,∠PCE=∠ACB=60°,
∴∠PCB=∠ACE,
∵BC=AC,∠PBC=∠CAE,
∴△ACE≌△PBC,
∴PB=AE,
∴PA=PB+PC.
点评:此题比较复杂,解答此题的关键是在PA上截取PE=PC,构造出等边三角形,再利用全等三角形的判定定理及性质解答即可.

练习册系列答案
相关题目
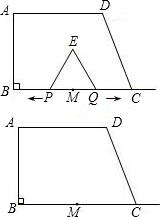 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,