题目内容
已知圆锥底面半径为5cm，侧面积为65πcm2，设母线与高的夹角为θ，则cosθ的值为 ．
考点：圆锥的计算
专题：计算题
分析：设圆锥的母线长为l，根据圆锥的侧面展开图为扇形和扇形的面积公式得到
•l•2π•5=65π，解得l=13，再根据勾股定理计算出圆锥的高，然后根据余弦的定义求解．
| 1 |
| 2 |
解答：解：设圆锥的母线长为l，
根据题意得
•l•2π•5=65π，解得l=13，
所以圆锥的高=
=12，
所以cosθ=
．
故答案为
．
根据题意得
| 1 |
| 2 |
所以圆锥的高=
| 132-52 |
所以cosθ=
| 12 |
| 13 |
故答案为
| 12 |
| 13 |
点评：本题考查了圆锥的计算：圆锥的侧面展开图为扇形，扇形的弧长等于圆锥底面圆的周长，扇形的半径等于圆锥的母线长．也考查了扇形的面积公式、勾股定理和锐角三角函数的定义．
练习册系列答案
一线名师提优试卷系列答案
相关题目
下列各数中，是无理数的是（ ）
| A、-1 | ||
| B、0 | ||
C、
| ||
D、
|
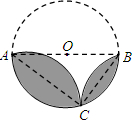如图，AB是⊙O的直径，点C在⊙O上，将弦AC、BC所对的劣弧分别沿AC、BC翻折，将AB上方所对的半圆沿AB翻折．若AC=4，BC=3，则翻折后的三条弧组成两个“叶片形”图形（阴影部分）的周长和为
为了了解某校九年级学生在第一次模拟考试中的数学成绩（满分120分），随机抽查了部分学生的错解（均为整数），整理并制作图表（均不完整）如下：若a=2b-2，则（a-2b+1）2013+（2b-a）0的值为（ ）
| A、-1 | B、0 | C、1 | D、无法确定 |