Question

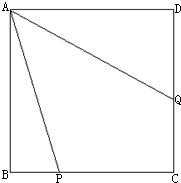25、如图，在正方形ABCD中，P、Q分别是BC、CD上的点，且∠PAQ=45°
（1）画出△ADQ按顺时针方向旋转90°后的△ABE；
（2）根据旋转的特征可知：AQ=

AE

，DQ=

PE

，∠DAQ=

∠BAE

；
（3）你能发现△AQP与△AEP具有哪种对称性吗？
（4）根据（3）的结论，请你说明PQ=PB+DQ．

Answer 1

分析：（1）做AE⊥AQ交CB的延长线于点E；
（2）找到对应线段与对应角即可；
（3）它们的对应点的连线交于一点，那么不是中心对称图形，一定是轴对称图形；
（4）易得PB+DQ=PE，证PE和PQ所在的三角形全等即可．

解答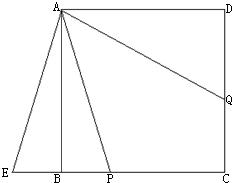：解：（1）2分．
（2）AE，PE，∠BAE；（每空1分）
（3）△AQP与△AEP都是轴对称图形；（1分）
（4）由旋转可知：△AQD≌△ABE，
∴AQ=AE，BE=DQ，∠DAQ=∠BAE，
∵∠PAQ=45°，∠BAD=90°，
∴∠DAQ+∠BAP=45°，
∴∠BAE+∠BAP=45°，
即：∠EAP=45°，
∴∠PAQ=∠EAP，
∵AP=AP，
∴△PAQ≌△PAE，
∴PQ=PE，
∴PQ=PB+DQ．（3分）

点评：用到的知识点为：旋转前后对应线段，对应角相等；证明两条线段相等，通常是证明这两条线段所在的三角形全等．