Question

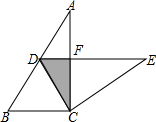
如图，在△ABC中，∠ACB=90°，∠A=30°，BC=2．将△ABC绕点C按顺时针方向旋转n度后得到△EDC，此时点D在AB边上，斜边DE交AC边于点F．
（1）求DC的长和旋转的角度n；
（2）求图中阴影部分的面积．

Answer 1

（1）根据旋转的性质可得DC=CB=2，
∵∠ACB=90°，∠A=30°，
∴∠B=90°-30°=60°，
∴△BCD是等边三角形，
∴旋转的角度n=∠BCD=60°；

（2）∵∠ACB=90°，∠A=30°，BC=2，
∴AB=2BC=4，
∴AD=4-2=2，
∴AD=CD，
∴∠A=∠DCA=30°，
又∵∠EDC=∠B=60°，
∴∠CFD=180°-30°-60°=90°，
∴DF⊥AC，
∵BC=2，AB=4，
∴AC=

42-22

=2

3

，
∴AF=FC=

1

2

AC=

3

，
∴DF=1，
阴影部分的面积=

1

2

AF•DF=

1

2

3

．