题目内容
 如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:
如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:
①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.
其中说法正确的结论有________.
①②③
分析:根据正方形的性质、直角三角形的性质、直角三角形面积的计算公式及勾股定理解答.
解答: 解:①∵△ABC为直角三角形,
解:①∵△ABC为直角三角形,
∴根据勾股定理:x2+y2=AB2=49,
故本选项正确;
②由图可知,x-y=CE= =2,
=2,
故本选项正确;
③由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,
列出等式为4× ×xy+4=49,
×xy+4=49,
即2xy+4=49;
故本选项正确;
④由2xy+4=49可得2xy=45①,
又∵x2+y2=49②,
∴①+②得,x2+2xy+y2=49+45,
整理得,(x+y)2=94,
x+y=±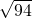 ≠9,
≠9,
故本选项错误.
∴正确结论有①②③.
故答案为①②③.
点评:本题考查了勾股定理及正方形和三角形的边的关系,此图被称为“弦图”,熟悉勾股定理并认清图中的关系是解题的关键.
分析:根据正方形的性质、直角三角形的性质、直角三角形面积的计算公式及勾股定理解答.
解答:
 解:①∵△ABC为直角三角形,
解:①∵△ABC为直角三角形,∴根据勾股定理:x2+y2=AB2=49,
故本选项正确;
②由图可知,x-y=CE=
 =2,
=2,故本选项正确;
③由图可知,四个直角三角形的面积与小正方形的面积之和为大正方形的面积,
列出等式为4×
 ×xy+4=49,
×xy+4=49,即2xy+4=49;
故本选项正确;
④由2xy+4=49可得2xy=45①,
又∵x2+y2=49②,
∴①+②得,x2+2xy+y2=49+45,
整理得,(x+y)2=94,
x+y=±
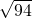 ≠9,
≠9,故本选项错误.
∴正确结论有①②③.
故答案为①②③.
点评:本题考查了勾股定理及正方形和三角形的边的关系,此图被称为“弦图”,熟悉勾股定理并认清图中的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( ) 如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有
如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有

