题目内容
Rt△ABC中,∠C=90°,BC=3,AC=4,斜边AB边上的高为CD,若以C为圆心,以3cm为半径作圆,则点D在________.
在⊙C内
分析:直角三角形中根据勾股定理可以计算AB的长度,CD为AB边上的高,根据面积法AC×BC=AB×DC可以求得CD的长,与半径比较后即可得到点D与圆的位置关系.
解答:直角△ABC中,AB2=AC2+BC2,
AC=4,BC=3,
∴AB= =5,
=5,
△ABC的面积S= •AC•BC=
•AC•BC= •AB•CD
•AB•CD
CD= =
= .
.
∵ <3,
<3,
∴点D在⊙C内,
故答案为:在⊙C内.
点评:本题考查了直角三角形中勾股定理的运用及点与圆的位置关系,根据勾股定理计算斜边长是解题的关键.
分析:直角三角形中根据勾股定理可以计算AB的长度,CD为AB边上的高,根据面积法AC×BC=AB×DC可以求得CD的长,与半径比较后即可得到点D与圆的位置关系.
解答:直角△ABC中,AB2=AC2+BC2,
AC=4,BC=3,
∴AB=
 =5,
=5,△ABC的面积S=
 •AC•BC=
•AC•BC= •AB•CD
•AB•CDCD=
 =
= .
.∵
 <3,
<3,∴点D在⊙C内,
故答案为:在⊙C内.
点评:本题考查了直角三角形中勾股定理的运用及点与圆的位置关系,根据勾股定理计算斜边长是解题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
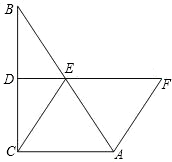 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=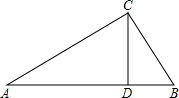 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=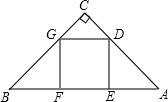 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为