题目内容
在△ABC中，∠BAC=90°，AD⊥BC于D，BD=3，AD=9，则AB2：AC2=________．
1：9
分析：由已知条件易证得△ADB∽△CAB，可得BD：AD=AB：AC，已知BD=3，AD=9，即可得AB2：AC2的值．
解答：∵∠BAC=90°，AD⊥BC，∠B为公共角，
∴△ADB∽△CAB，即BD：AD=AB：AC，
∵BD=3，AD=9，
∴
=
，
∴
=（
）2=
．故答案填1：9．
点评：本题主要考查了直角三角形相似的判定，找到相应等量关系的边是正确解题的关键．
分析：由已知条件易证得△ADB∽△CAB，可得BD：AD=AB：AC，已知BD=3，AD=9，即可得AB2：AC2的值．
解答：∵∠BAC=90°，AD⊥BC，∠B为公共角，
∴△ADB∽△CAB，即BD：AD=AB：AC，
∵BD=3，AD=9，
∴
=，∴
=（）2=．故答案填1：9．点评：本题主要考查了直角三角形相似的判定，找到相应等量关系的边是正确解题的关键．
练习册系列答案
相关题目
；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x．
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿AB以4cm/s的速度向点B运动，同时点Q从C点出发，沿CA以3cm/s的速度向点A运动，设运动时间为x秒．
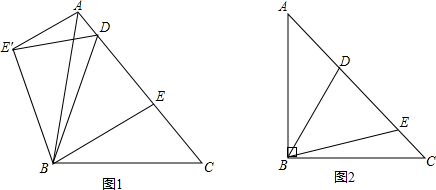
如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿AB以每秒4cm，的速度向点B运动，同时点Q从C点出发，沿CA以3cm/s的速度向点A运动，设运动时间为x秒．