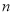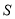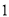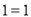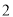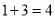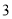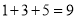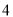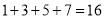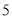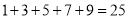题目内容
两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,…那么六条直线最多有( )
A. 21个交点 B. 18个交点 C. 15个交点 D. 10个交点
C 【解析】试题分析:由题意两条直线最多有个交点,三条直线最多有个交点,四条直线最多有个交点,根据这个规律即可求得结果. 由题意得六条直线最多有个交点,故选C.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
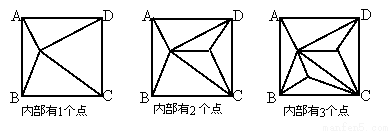
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
(1)填表详见解析;(2)能;1007个. 【解析】 试题分析:(1)查出题干图形中三角形的个数,并观察发现,每多一个点,三角形的个数增加2,据此规律填表即可; (2)根据(1)中规律,列式求解,如果n是整数,则能分割,如果n不是整数,则不能分割. 试题解析:(1)填表如下: 正方形ABCD内点的个数 1 2 3 4 … n ...从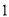 开始,连续的奇数相加,它们和的情况如表所示:
开始,连续的奇数相加,它们和的情况如表所示:
加数的个数 | 连续奇数的和 |
|
|
|
|
|
|
|
|
|
|
|
|
(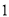 )当
)当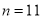 时,
时, 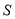 的值为__________.
的值为__________.
(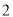 )用含
)用含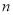 的代数式表示
的代数式表示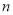 个连续奇数之和
个连续奇数之和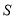 的公式,
的公式, 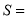 __________.
__________.
用含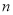 的代数式表示从
的代数式表示从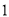 开始的第
开始的第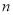 个连续奇数是__________.
个连续奇数是__________.
(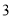 )根据规律计算
)根据规律计算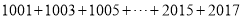 .
.