题目内容
已知：abc＞0，
＞0，a+b＜0，x=
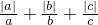，则x3+2x2-2=________．
-1
分析：根据＞0，a+b＜0，可知a＜0，b＜0，又由abc＞0可知c＞0，依此先求出x的值，再代入求出x3+2x2-2的值．
解答：∵＞0，a+b＜0，
∴a＜0，b＜0，
又∵abc＞0，
∴c＞0，
∴x=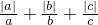=-1-1+1=-1，
∴x3+2x2-2=（-1）3+2×（-1）2-2=-1．
故答案为：-1．
点评：本题考查了代数式求值，解题关键是根据已知得出a＜0，b＜0，c＞0，从而求出x的值．
分析：根据
＞0，a+b＜0，可知a＜0，b＜0，又由abc＞0可知c＞0，依此先求出x的值，再代入求出x3+2x2-2的值．解答：∵
＞0，a+b＜0，∴a＜0，b＜0，
又∵abc＞0，
∴c＞0，
∴x=
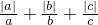=-1-1+1=-1，∴x3+2x2-2=（-1）3+2×（-1）2-2=-1．
故答案为：-1．
点评：本题考查了代数式求值，解题关键是根据已知得出a＜0，b＜0，c＞0，从而求出x的值．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
20、已知直角△ABC中∠B=90°，延长BC到D，使CD=AB，过D作BD的垂线，在这个垂线上截取DE=BC．求证：AC⊥EC．
如图，已知三角形△ABC中，∠A=90°，AB=3，BC=6．
如图所示，已知在△ABC中，BC=4cm，把△ABC沿BC方向平移2cm得到△DEF．问：