题目内容
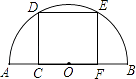
【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在 ![]() 上且不与A点重合,但Q点可与B点重合.
上且不与A点重合,但Q点可与B点重合. 
发现: ![]() 的长与
的长与 ![]() 的长之和为定值l,求l:
的长之和为定值l,求l:
【答案】解:如图1,连接OP、OQ, 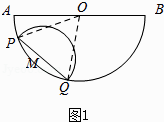
∵AB=4,
∴OP=OQ=2,
∵PQ=2,
∴△OPQ是等边三角形,
∴∠POQ=60°,
∴ ![]() =
= ![]() =
= ![]() ,
,
又∵半圆O的长为: ![]() π×4=2π,
π×4=2π,
∴ ![]() +
+ ![]() =2π﹣
=2π﹣ ![]() π=
π= ![]() ,
,
∴l= ![]() π;
π;
思考:点M与AB的最大距离为 , 此时点P,A间的距离为 ;
点M与AB的最小距离为 , 此时半圆M的弧与AB所围成的封闭图形面积为 ;![]() |2||
|2|| ![]()
![]() ﹣
﹣ ![]()
探究:当半圆M与AB相切时,求 ![]() 的长.
的长.
(注:结果保留π,cos35°= ![]() ,cos55°=
,cos55°= ![]() )
)
解:当半圆M与AB相切时,
此时,MC=1,
如图4,当点C在线段OA上时,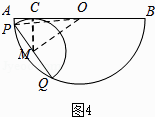
在Rt△OCM中,
由勾股定理可求得:OC= ![]() ,
,
∴cos∠AOM= ![]() =
= ![]() ,
,
∴∠AOM=35°,
∵∠POM=30°,
∴∠AOP=∠AOM﹣∠POM=5°,
∴ ![]() =
= ![]() =
= ![]() ,
,
当点C在线段OB上时,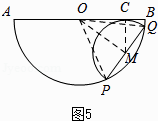
此时,∠BOM=35°,
∵∠POM=30°,
∴∠AOP=180°﹣∠POM﹣∠BOM=115°
∴ ![]() =
= ![]() =
= ![]() ,
,
综上所述,当半圆M与AB相切时, ![]() 的长为
的长为 ![]() 或
或 ![]() .
.
【解析】解:发现: 思考:如图2,过点M作MC⊥AB于点C,
连接OM,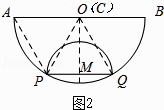
∵OP=2,PM=1,
∴由勾股定理可知:OM= ![]() ,
,
当C与O重合时,
M与AB的距离最大,最大值为 ![]() ,
,
连接AP,
此时,OM⊥AB,
∴∠AOP=60°,
∵OA=OP,
∴△AOP是等边三角形,
∴AP=2,
如图3,当Q与B重合时,
连接DM,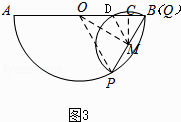
∵∠MOQ=30°,
∴MC= ![]() OM=
OM= ![]() ,
,
此时,M与AB的距离最小,最小值为 ![]() ,
,
设此时半圆M与AB交于点D,
DM=MB=1,
∵∠ABP=60°,
∴△DMB是等边三角形,
∴∠DMB=60°,
∴扇形DMB的面积为: ![]() =
= ![]() ,
,
△DMB的面积为: ![]() MCDB=
MCDB= ![]() ×
× ![]() ×1=
×1= ![]() ,
,
∴半圆M的弧与AB所围成的封闭图形面积为: ![]() ﹣
﹣ ![]() ;
;

 名校课堂系列答案
名校课堂系列答案