题目内容
【题目】设抛物线的解析式为y=ax2 ， 过点B1（1，0）作x轴的垂线，交抛物线于点A1（1，2）；过点B2（ 
，0）作x轴的垂线，交抛物线于点A2；…；过点Bn（（ ）n﹣1 ， 0）（n为正整数）作x轴的垂线，交抛物线于点An ， 连接AnBn+1 ， 得Rt△AnBnBn+1 ．
（1）求a的值；
（2）直接写出线段AnBn ， BnBn+1的长（用含n的式子表示）；
（3）在系列Rt△AnBnBn+1中，探究下列问题：
①当n为何值时，Rt△AnBnBn+1是等腰直角三角形？
②设1≤k＜m≤n（k，m均为正整数），问：是否存在Rt△AkBkBk+1与Rt△AmBmBm+1相似？若存在，求出其相似比；若不存在，说明理由．
【答案】
（1）
解：如图1所示，
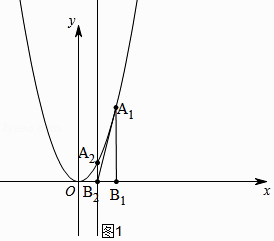
∵点A1（1，2）在抛物线的解析式为y=ax2上，
∴a=2
（2）
解：如图2所示，
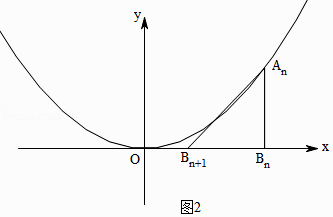
AnBn=2x2=2×[（ 
）n﹣1]2= 
，BnBn+1= 
（3）
解：如图3所示，
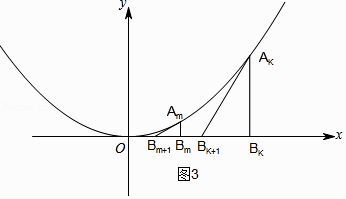
由Rt△AnBnBn+1是等腰直角三角形得AnBn=BnBn+1，则： = ，
2n﹣3=n，n=3，
∴当n=3时，Rt△AnBnBn+1是等腰直角三角形，
②依题意得，∠AkBkBk+1=∠AmBmBm+1=90°，
有两种情况：i）当Rt△AkBkBk+1∽Rt△AmBmBm+1时，
= 
， 
= 
， 
= 
，
所以，k=m（舍去），
ii）当Rt△AkBkBk+1∽Rt△Bm+1BmAm时，
= 
， 
= 
， 
= 
，
∴k+m=6，
∵1≤k＜m≤n（k，m均为正整数），
∴取 
或 
；
当 时，Rt△A1B1B2∽Rt△B6B5A5，
相似比为： 
= 
=64，
当 时，Rt△A2B2B3∽Rt△B5B4A4，
相似比为： 
= 
=8，
所以：存在Rt△AkBkBk+1与Rt△AmBmBm+1相似，其相似比为64：1或8：1．
【解析】（1）直接把点A1的坐标代入y=ax2求出a的值；（2）由题意可知：A1B1是点A1的纵坐标：则A1B1=2×12=2；A2B2是点A2的纵坐标：则A2B2=2×（ ）2= ；…则AnBn=2x2=2×[（ ）n﹣1]2= ；
B1B2=1﹣ = ，B2B3= ﹣ 
= 
= ，…，BnBn+1= ；（3）因为Rt△AkBkBk+1与Rt△AmBmBm+1是直角三角形，所以分两种情况讨论：根据（2）的结论代入所得的对应边的比列式，计算求出k与m的关系，并与1≤k＜m≤n（k，m均为正整数）相结合，得出两种符合条件的值，分别代入两相似直角三角形计算相似比．
