题目内容
12、若△ABC的边长a，b，c满足a2+b2+c2+50=6a+8b+10c，那么△ABC是（ ）
分析：a2+b2+c2+50=6a+8b+10c可变为（a-3）2+（b-4）2+（c-5）2=0，可知道a、b、c分别为3，4，5满足勾股定理，即可判断出三角形的形状．
解答：解：a2+b2+c2+50=6a+8b+10c变形为
（a-3）2+（b-4）2+（c-5）2=0
解之得：a=3，b=4，c=5，
符合勾股定理的逆定理，
故选B．
（a-3）2+（b-4）2+（c-5）2=0
解之得：a=3，b=4，c=5，
符合勾股定理的逆定理，
故选B．
点评：本题考查了勾股定理逆定理的应用，是基础知识，较简单．
练习册系列答案
名校课堂系列答案
相关题目
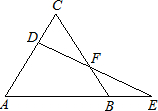如图，△ABC是等边三角形，D为AC边上的一个动点，延长AB到E，使BE=CD，连接DE交BC于F．
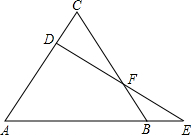如图，△ABC是等边三角形，D为AC边上的一个动点，延长AB到E，使BE=CD，连接DE交BC于F．