题目内容
 如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.(1)试探究,四边形BECF是什么特殊的四边形并证明之;
(2)当∠A的大小满足什么条件时四边形BECF是正方形?并证明你的结论.
(3)若四边形BECF的面积是6(cm)2且BC+AC=
| 105 |
分析:(1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC,又因为CF=AE,BE=EC=BF=FC,根据四边相等的四边形是菱形,所以四边形BECF是菱形;
(2)由菱形的性质知,对角线平分一组对角,即当∠ABC=45°时,∠EBF=90°,有菱形为正方形,根据直角三角形中两个角锐角互余得,∠A=45度;
(3)根据菱形的面积公式可知:BC•EF=6×2(cm)2,又BC+AC=
cm,再根据勾股定理即可求出BE的长,继而得出AB的长.
(2)由菱形的性质知,对角线平分一组对角,即当∠ABC=45°时,∠EBF=90°,有菱形为正方形,根据直角三角形中两个角锐角互余得,∠A=45度;
(3)根据菱形的面积公式可知:BC•EF=6×2(cm)2,又BC+AC=
| 105 |
解答:解:(1)四边形BECF是菱形.
证明:EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠3=∠1,
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,
∴∠2=∠4,
∴EC=AE,
∴BE=AE,
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明:∵∠A=45°,∠ACB=90°,
∴∠1=45°,
∴∠EBF=2∠A=90°,
∴菱形BECF是正方形.
(3)∵CF=AE,四边形BECF是菱形,
∴CF
AE,
∴四边形AEFC为平行四边形,
∴EF=AC,
根据菱形的面积公式可知:
=6(cm)2,
∴BC•AC=6×2=12(cm)2,
又∵BC+AC=
cm,
∴(BC+AC)2-2BC•AC=BC2+AC2=105-2×12=81(cm)2,
∴AB=2BE=2×
=9cm.
证明:EF垂直平分BC,
∴BF=FC,BE=EC,

∴∠3=∠1,
∵∠ACB=90°,
∴∠3+∠4=90°,∠1+∠2=90°,
∴∠2=∠4,
∴EC=AE,
∴BE=AE,
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明:∵∠A=45°,∠ACB=90°,
∴∠1=45°,
∴∠EBF=2∠A=90°,
∴菱形BECF是正方形.
(3)∵CF=AE,四边形BECF是菱形,
∴CF
| ∥ |
. |
∴四边形AEFC为平行四边形,
∴EF=AC,
根据菱形的面积公式可知:
| BC•AC |
| 2 |
∴BC•AC=6×2=12(cm)2,
又∵BC+AC=
| 105 |
∴(BC+AC)2-2BC•AC=BC2+AC2=105-2×12=81(cm)2,
∴AB=2BE=2×
|
点评:本题考查菱形的判定和性质,以及正方形的判定,有一定难度,解题关键是熟练掌握菱形的判定方法及性质并灵活运用.

练习册系列答案
相关题目
 如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.
如图,已知在四边形ABCD中,AD=AB,CD=CB,则∠D=∠B,试说明理由.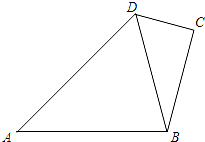 如图,已知在四边形ABCD中,∠C=90°,AB=AD=10,cos∠ABD=
如图,已知在四边形ABCD中,∠C=90°,AB=AD=10,cos∠ABD= 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.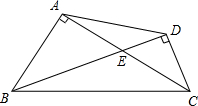 (2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25.
(2013•奉贤区一模)如图,已知在四边形ABCD中,AC⊥AB,BD⊥CD,AC与BD相交于点E,S△AED=9,S△BEC=25. 如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.
如图,已知在四边形ABCD中,∠ABC=2∠ADC=2a,点E、F分别在CB、CD的延长线上,且EB=AB+AD,∠AEB=∠FAD,猜想线段AE、AF的数量关系,并证明你的猜想.