题目内容

若等腰直角三角形的斜边长为2，则它的面积为

A.
$数学公式$
B.
1
C.
2
D.
$数学公式$

B
分析：设等腰直角三角形的直角边为xcm，根据等腰直角三角形的性质及勾股定理可求得直角边的长，从而不难求得其面积．
解答：设等腰直角三角形的直角边为xcm，则其斜边长为 $\text{[math]}$ xcm，
∵ $\text{[math]}$ x=2
∴x= $\text{[math]}$ ，
∴该三角形的面积= $\text{[math]}$ × $\text{[math]}$ × $\text{[math]}$ =1．
故选B．
点评：此题主要考查学生对等腰直角三角形的性质及勾股定理的运用．解答该题时，注意将隐含在题干中的已知条件：等腰直角三角形的两条直角边相等，挖掘出来．

练习册系列答案

通城学典初中课外文言文阅读系列答案

名师学案英语阅读系列答案

口算题卡加应用题一日一练系列答案

53题霸专题集训系列答案

中考现代文阅读系列答案

语文全真模拟试卷系列答案

小学数学知识集锦系列答案

实战演练卷系列答案

口算小状元口算速算天天练系列答案

优才精英口算题卡应用题系列答案

相关题目

23、如图①，将一张直角三角形纸片△ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形；再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”．
（1）如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；
（2）如图③，在正方形网格中，以给定的BC为一边，画出一个斜三角形ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；
（3）若一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？

在平面直角坐标系中，现将一块等腰直角三角板放在第一象限，斜靠在两坐标轴上，且

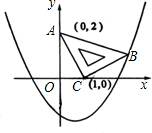点A（0，2），点C（1，0），如图所示，抛物线y=ax²-ax-2经过点B．
（1）求点B的坐标；
（2）求抛物线的解析式；
（3）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中，将一块腰长为

的等腰直角三角板ABC放在第二象

限，且斜靠在两坐标轴上，直角顶点C的坐标为（-1，0），点B在抛物线y=ax²+ax-2上．
（1）点A的坐标为

，点B的坐标为

；
（2）抛物线的解析式为

；
（3）设（2）中抛物线的顶点为D，求△DBC的面积；
（4）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．

在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点A（0，2），C（-1，0），如图所示．
（1）求点B的坐标；
（2）若以（-

）为顶点的抛物线经过点B，求该抛物线的解析式；
（3）在（2）中的抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．

如图所示，在平面直角坐标系中，现将一张等腰直角三角形纸片ABC放在第二象限，斜靠在

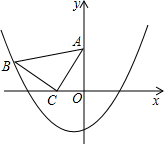两坐标轴上，点B的坐标为（-3，1），且抛物线y=ax²+ax-4a经过点B．
（Ⅰ）求抛物线的解析式；
（Ⅱ）求点A和点C的坐标；
（Ⅲ）以AC所在直线为对称轴，将△ABC折叠，问点B的对称点B₁是否落在抛物线上？再以AC的中点为对称中心，将△ABC作中心对称变换，这时点B的对称点B₂是否落在抛物线上？若在，求出它们的坐标；若不在，请说明理由．