��Ŀ����
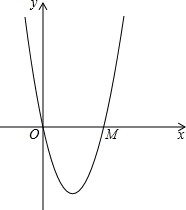
��ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��a��0����x�ύ�ڵ�O��M���Գ���Ϊֱ��x=2����OMΪֱ����ԲA����OM�ij�Ϊ�߳�������ABCD���ҵ�B��C�ڵ������ޣ���C�������߶Գ����ϣ���D��y�Ḻ�����ϣ�
��1����֤��4a+b=0��
��2����ԲA���߶�AB�Ľ���ΪE�����ж�ֱ��DE��ԲA��λ�ù�ϵ����˵��������ɣ�
��3���������߶���P������ABCD���ڲ��ҡ�OPMΪ���ʱ����a��ȡֵ��Χ��
�����㡿���κ����ۺ��⣮
����������1���������֪��4��0�����������߾�����O�����c=0����c=0��x=4��y=0���������ߵĽ���ʽ��֤�ã�4a+b=0��
��2����ͼ1��ʾ�������ε����ʿ�֪��DN=NB��DN��AN����OM=AD=AB����֤��AD=AB=DB����AE=2��֪AE=EB���ɵ������������ߺ�һ�����ʿ�֪AE��DE���Ӷ���֤��DE��ԲA���У�
��3����ͼ2��ʾ�����P������Ϊ��2��m�����������֪��E������Ϊ��﹣2��2�����������ߵĽ���ʽΪy=ax��x﹣4������x=2�����y=﹣4a��m=﹣4a���ɡ�OPMΪ����������ߵĶ��������ε��ڲ���֪﹣4a��﹣2��﹣4a��﹣4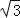 ���Ӷ������a��ȡֵ��Χ��
���Ӷ������a��ȡֵ��Χ��
����𡿽⣺��1����O������Ϊ��0��0���������ߵĶԳ���Ϊx=2��
���M��������4��0����
�������߾�����O��
��c=0��
��c=0��x=4��y=0���������ߵĽ���ʽ�ã�16a+4b=0��
�����ã�4a+b=0��
��2��DE��ԲA���У�
���ɣ���ͼ1��ʾ��
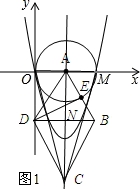
���ı���ABCDΪ���Σ�
��DN=NB��DN��AN��
�ߡ�AOD=��AON=��DNA=90�㣬
���ı���OANDΪ���Σ�
��OA=DN=2��
��DB=OM=4��
��OM=AD=AB��
��AD=AB=DB��
��AEΪԲA�İ뾶��
��AE=EB=2��
��AD=DB��AE=EB��
��AE��DE��
��DE��ԲA���У�
��3����ͼ2��ʾ��
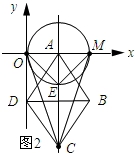
���P��������2��m����
��OMΪԲA��ֱ����
���OEM=90�㣮
��AE=2��OA=2��
���E������Ϊ��﹣2��2����
�������ߵĽ���ʽΪy=ax��x﹣4������x=2�����y=﹣4a��
��m=﹣4a��
�ߡ�OPMΪ��ǣ�
���P�ڵ�E���·���
��﹣4a��﹣2��
��ã�a��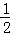 ��
��
��Rt��AOD��OD=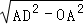 =2
=2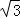 ��
��
��AC=4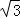 ��
��
�ߵ�P�����ε��ڲ���
���P�ڵ�C���Ϸ���
��﹣4a��﹣4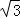 ��
��
��ã�a��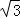 ��
��
��a��ȡֵ��Χ��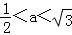 ��
��
��������������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ�������ε����ʡ����ߵ��ж����ȱ������ε����ʺ��ж����������������ߺ�һ�����ʣ����������������ߺ�һ������֤��DE��AE�ǽ�����⣨2���Ĺؼ����������ߵĶ���P������ABCD���ڲ��ҡ�OPMΪ��ǵó���P���������ȡֵ��Χ�ǽ����⣨3���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
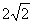 (D)
(D)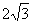

 B��
B��

