题目内容
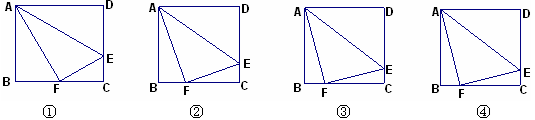
如下4个图中,不同的矩形ABCD,若把D点沿AE对折,使D点与BC上的F点重合;
(1)图①中,若DE:EC=2:1,求证:△ABF∽△AFE∽△FCE;并计算BF:FC.
(2)图②中若DE:EC=3:1,计算BF:FC=
(3)图④中若DE:EC=n:1,猜想BF:FC=

(1)图①中,若DE:EC=2:1,求证:△ABF∽△AFE∽△FCE;并计算BF:FC.
(2)图②中若DE:EC=3:1,计算BF:FC=
1:2
1:2
;图③中若DE:EC=4:1,计算BF:FC=1:3
1:3
.(3)图④中若DE:EC=n:1,猜想BF:FC=
1:(n-1)
1:(n-1)
;并证明你的结论.分析:(1)由矩形ABCD,DE:EC=2:1,把D点沿AE对折,使D点与BC上的F点重合;易求得∠BAF=∠FAE=∠CFE=30°,∠B=∠C=∠AFE=90°,即可证得:△ABF∽△AFE∽△FCE;首先设CE=x,则EF=DE=2x,CD=DE+CE=3x,由勾股定理即可求得FC的长,又由相似三角形的对应边成比例,可求得BF的长,继而求得答案;
(2)首先设CE=x,由DE:EC=3:1,可得EF=DE=3x,CD=DE+CE=4x,由勾股定理即可求得FC的长,又由相似三角形的对应边成比例,可求得BF的长,继而求得答案;
首先设CE=x,由DE:EC=4:1,可得EF=DE=4x,CD=DE+CE=5x,由勾股定理即可求得FC的长,又由相似三角形的对应边成比例,可求得BF的长,继而求得答案;
(3)首先设CE=x,由DE:EC=n:1,可得EF=DE=nx,CD=DE+CE=(n+1)x,由勾股定理即可求得FC的长,又由相似三角形的对应边成比例,可求得BF的长,继而求得答案.
(2)首先设CE=x,由DE:EC=3:1,可得EF=DE=3x,CD=DE+CE=4x,由勾股定理即可求得FC的长,又由相似三角形的对应边成比例,可求得BF的长,继而求得答案;
首先设CE=x,由DE:EC=4:1,可得EF=DE=4x,CD=DE+CE=5x,由勾股定理即可求得FC的长,又由相似三角形的对应边成比例,可求得BF的长,继而求得答案;
(3)首先设CE=x,由DE:EC=n:1,可得EF=DE=nx,CD=DE+CE=(n+1)x,由勾股定理即可求得FC的长,又由相似三角形的对应边成比例,可求得BF的长,继而求得答案.
解答:(1)证明:如图①,∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
由折叠的性质可得:FE=DE,∠AFE=∠D=90°,∠DAE=∠FAE,
∵DE:EC=2:1,
∴EF=2EC,
∴∠EFC=30°,
∴∠EFB=60°,
∴∠BAF=30°,
∴∠FAE=∠EAD=30°,
∴∠BAF=∠FAE=∠CFE=30°,
∵∠B=∠C=∠AFE=90°,
∴△ABF∽△AFE∽△FCE;
设CE=x,则EF=DE=2x,CD=DE+CE=3x,
∴FC=
=
x,
∵AB=CD=3x,△ABF∽△FCE,
∴
=
,
∴
=
,
解得:BF=
x,
∴BF:FC=1:1;
(2)解:如图②,设CE=x,
∵DE:EC=3:1,
∴EF=DE=3x,CD=DE+CE=4x,
∴FC=
=2
x,
∵AB=CD=4x,△ABF∽△FCE,
∴
=
,
∴
=
,
解得:BF=
x,
∴BF:FC=1:2;
如图③,设CE=x,
∵DE:EC=4:1,
∴EF=DE=4x,CD=DE+CE=5x,
∴FC=
=
x,
∵AB=CD=5x,△ABF∽△FCE,
∴
=
,
∴
=
,
解得:BF=
x,
∴BF:FC=1:3;
故答案为:1:2,1:3;
(3)证明:如图④,设CE=x,
∵DE:EC=n:1,
∴EF=DE=nx,CD=DE+CE=(n+1)x,
∴FC=
=
x,
∵AB=CD=(n+1)x,△ABF∽△FCE,
∴
=
,
∴
=
,
解得:BF=
x,
∴BF:FC=1:(n-1);
故答案为:1:(n-1).
∴∠B=∠C=∠D=90°,
由折叠的性质可得:FE=DE,∠AFE=∠D=90°,∠DAE=∠FAE,
∵DE:EC=2:1,
∴EF=2EC,
∴∠EFC=30°,
∴∠EFB=60°,
∴∠BAF=30°,
∴∠FAE=∠EAD=30°,
∴∠BAF=∠FAE=∠CFE=30°,
∵∠B=∠C=∠AFE=90°,
∴△ABF∽△AFE∽△FCE;
设CE=x,则EF=DE=2x,CD=DE+CE=3x,
∴FC=
| EF2-CE2 |
| 3 |
∵AB=CD=3x,△ABF∽△FCE,
∴
| AB |
| FC |
| BF |
| EC |
∴
| 3x | ||
|
| BF |
| x |
解得:BF=
| 3 |
∴BF:FC=1:1;
(2)解:如图②,设CE=x,
∵DE:EC=3:1,
∴EF=DE=3x,CD=DE+CE=4x,
∴FC=
| EF2-CE2 |
| 2 |
∵AB=CD=4x,△ABF∽△FCE,
∴
| AB |
| FC |
| BF |
| EC |
∴
| 4x | ||
2
|
| BF |
| x |
解得:BF=
| 2 |
∴BF:FC=1:2;
如图③,设CE=x,
∵DE:EC=4:1,
∴EF=DE=4x,CD=DE+CE=5x,
∴FC=
| EF2-CE2 |
| 15 |
∵AB=CD=5x,△ABF∽△FCE,
∴
| AB |
| FC |
| BF |
| EC |
∴
| 5x | ||
|
| BF |
| x |
解得:BF=
| ||
| 3 |
∴BF:FC=1:3;
故答案为:1:2,1:3;
(3)证明:如图④,设CE=x,
∵DE:EC=n:1,
∴EF=DE=nx,CD=DE+CE=(n+1)x,
∴FC=
| EF2-CE2 |
| n2-1 |
∵AB=CD=(n+1)x,△ABF∽△FCE,
∴
| AB |
| FC |
| BF |
| EC |
∴
| (n+1)x | ||
|
| BF |
| x |
解得:BF=
| ||
| n-1 |
∴BF:FC=1:(n-1);
故答案为:1:(n-1).
点评:此题考查了相似三角形的判定与性质、矩形的性质、直角三角形的性质以及勾股定理.此题难度较大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目




 ︰1,猜想BF︰FC= ;并证明你的结论
︰1,猜想BF︰FC= ;并证明你的结论