题目内容
(1)计算: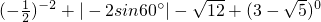
(2)解方程:2x2-4x-5=0(配方法)
(3)先化简,再求值: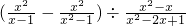 ,其中x是方程3x2-x-1=0的根.
,其中x是方程3x2-x-1=0的根.
解:(1)原式=4+ -2
-2 +1
+1
=5- ;
;
(2)由原方程,得
x2-2x- =0,
=0,
移项,得
x2-2x= ,
,
两边同时加上一次项系数的一半的平方,得
x2-2x+1= ,即(x-1)2=
,即(x-1)2= ,
,
开方,得
x-1=±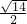 ,
,
解得x1=1+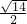 ,x2=1-
,x2=1-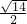 ;
;
(3)∵3x2-x-1=0,
∴3x2=x+1,
∴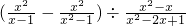 =
=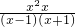 ×
×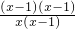 =
=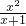 =
=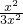 =
= ,即
,即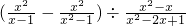 =
= .
.
分析:(1)先计算负整数指数幂、去绝对值、化简二次根式、零指数幂;然后根据实数运算法则进行计算;
(2)化二次项系数为1,把常数项-5移项后,应该在左右两边同时加上一次项系数的一半的平方.
(3)先化简所求代数式,然后3x2,=x+1代入求值即可.
点评:本题考查了实数的运算,配方法解方程等.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
 -2
-2 +1
+1=5-
 ;
;(2)由原方程,得
x2-2x-
 =0,
=0,移项,得
x2-2x=
 ,
,两边同时加上一次项系数的一半的平方,得
x2-2x+1=
 ,即(x-1)2=
,即(x-1)2= ,
,开方,得
x-1=±
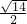 ,
,解得x1=1+
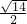 ,x2=1-
,x2=1-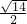 ;
;(3)∵3x2-x-1=0,
∴3x2=x+1,
∴
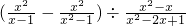 =
=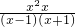 ×
×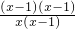 =
=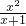 =
=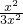 =
= ,即
,即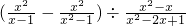 =
= .
.分析:(1)先计算负整数指数幂、去绝对值、化简二次根式、零指数幂;然后根据实数运算法则进行计算;
(2)化二次项系数为1,把常数项-5移项后,应该在左右两边同时加上一次项系数的一半的平方.
(3)先化简所求代数式,然后3x2,=x+1代入求值即可.
点评:本题考查了实数的运算,配方法解方程等.配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
