题目内容
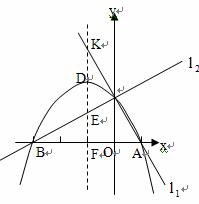
已知两直线![]() ,
,![]() 分别经过点A(1,0),点B
分别经过点A(1,0),点B![]() ,并且当两直线同时相交于y正半轴的点C时,恰好有
,并且当两直线同时相交于y正半轴的点C时,恰好有![]() ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线![]() 交于点K,如图所示。
交于点K,如图所示。
(1)求点C的坐标,并求出抛物线的函数解析式;
|
依次截得三条线段,问这三条线段有何数量关系?请说明理由。
(3)当直线![]() 绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
(1)解法1:由题意易知:△BOC∽△COA
∴![]() ,即
,即![]()
∴![]()
∴点C的坐标是(0,![]() )
)
由题意,可设抛物线的函数解析式为![]()
把A(1,0),B(![]() ,0)的坐标分别代入
,0)的坐标分别代入![]() ,得
,得

解这个方程组,得
∴抛物线的函数解析式为![]()
解法2:由勾股定理,得![]()
又∵OB=3,OA=1,AB=4
∴![]()
∴点C的坐标是(0,![]() )
)
由题意可设抛物线的函数解析式为![]() ,把C(0,
,把C(0,![]() )代入
)代入
函数解析式得![]()
所以,抛物线的函数解析式为![]()
(2)解法1:截得三条线段的数量关系为KD=DE=EF
理由如下:
可求得直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]()
抛物线的对称轴为直线![]()
由此可求得点K的坐标为(![]() ,
,![]() ),点D的坐标为(
),点D的坐标为(![]() ,
,![]() ),点E的坐标为(
),点E的坐标为(![]() ,
,![]() ),点F的坐标为(
),点F的坐标为(![]() ,0)
,0)
∴KD=![]() ,DE=
,DE=![]() ,EF=
,EF=![]()
∴KD=DE=EF
解法2:截得三条线段的数量关系为KD=DE=EF
理由如下:
由题意可知Rt△ABC中,∠ABC=30°,∠CAB=60°,则可得
![]() ,
,![]() ,
,
由顶点D坐标(![]() ,
,![]() )得
)得![]()
∴KD=DE=EF=![]()
(3)解法1:(i)以点K为圆心,线段KC长为半径画圆弧,交抛物线于点![]() ,由抛物线对称性可知点
,由抛物线对称性可知点![]() 为点C关于直线
为点C关于直线![]() 的对称点
的对称点
∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),此时△
),此时△![]() 为等腰三角形
为等腰三角形
(ii)当以点C为圆心,线段CK长为半径画圆弧时,与抛物线交点为点![]() 和点A,而三点A、C、K在同一直线上,不能构成三角形
和点A,而三点A、C、K在同一直线上,不能构成三角形
(iii)作线段KC的中垂线l,由点D是KE的中点,且![]() ,可知l经过点D,
,可知l经过点D,
∴KD=DC
此时,有点![]() 即点D坐标为(
即点D坐标为(![]() ,
,![]() ),使△
),使△![]() 为等腰三角形;
为等腰三角形;
综上所述,当点M的坐标分别为(![]() ,
,![]() ),(
),(![]() ,
,![]() )时,△MCK为等腰三角形。
)时,△MCK为等腰三角形。
解法2:当点M的坐标分别为(![]() ,
,![]() ),(
),(![]() ,
,![]() )时,△MCK为等腰三角形。
)时,△MCK为等腰三角形。
理由如下:
(i)连接BK,交抛物线于点G,易知点G的坐标为(![]() ,
,![]() )
)
又∵点C的坐标为(0,![]() ),则GC∥AB
),则GC∥AB
∵可求得AB=BK=4,且∠ABK=60°,即△ABK为正三角形
∴△CGK为正三角形
∴当![]() 与抛物线交于点G,即
与抛物线交于点G,即![]() ∥AB时,符合题意,此时点
∥AB时,符合题意,此时点![]() 的坐标为(
的坐标为(![]() ,
,![]() )
)
(ii)连接CD,由KD=![]() ,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形
,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形
∴当![]() 过抛物线顶点D时,符合题意,此时点
过抛物线顶点D时,符合题意,此时点![]() 坐标为(
坐标为(![]() ,
,![]() )
)
(iii)当点M在抛物线对称轴右边时,只有点M与点A重合时,满足CM=CK,但点
A、C、K在同一直线上,不能构成三角形
综上所述,当点M的坐标分别为(![]() ,
,![]() ),(
),(![]() ,
,![]() )时,△MCK为等腰三
)时,△MCK为等腰三
角形。

 已知两直线l1,l2分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点D,如图所示.
已知两直线l1,l2分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点D,如图所示. (2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.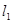 ,
,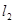 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有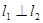 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线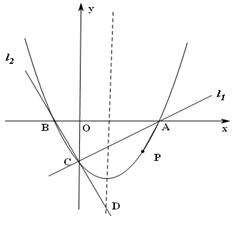
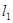 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;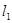 ,
, 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有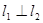 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线
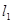 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;