题目内容
 如图,O是边长为1的正△ABC的中心,将△ABC绕点O逆时针方向旋转180°,得△A1B1C1,则△A1B1C1与△ABC重叠部分(图中阴影部分)的面积为( )
如图,O是边长为1的正△ABC的中心,将△ABC绕点O逆时针方向旋转180°,得△A1B1C1,则△A1B1C1与△ABC重叠部分(图中阴影部分)的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据旋转的性质,观察图形易得,图中空白部分的小三角形也是等边三角形,且边长为
,且面积是△ABC的
.重叠部分的面积是△ABC与三个小等边三角形的面积之差,代入数据计算可得答案.
| 1 |
| 3 |
| 1 |
| 9 |
解答:解:根据旋转的性质可知,图中空白部分的小三角形也是等边三角形,且边长为
,且面积是△ABC的
,
观察图形可得,重叠部分的面积是△ABC与三个小等边三角形的面积之差,
∴△ABC的高是
,一个小等边三角形的高是
,
∴△ABC的面积是
×1×
=
,一个小等边三角形的面积是
×
×
=
,
所以重叠部分的面积是
-
×3=
.
故选B.
| 1 |
| 3 |
| 1 |
| 9 |
观察图形可得,重叠部分的面积是△ABC与三个小等边三角形的面积之差,
∴△ABC的高是
| ||
| 2 |
| ||
| 6 |
∴△ABC的面积是
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 36 |
所以重叠部分的面积是
| ||
| 4 |
| ||
| 36 |
| ||
| 6 |
故选B.
点评:本题考查了图形的旋转变化,三角形面积的求法,难度不大,但容易错.

练习册系列答案
相关题目
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )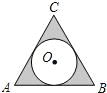 如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为
如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为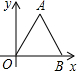 如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A
如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A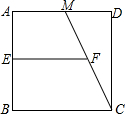 如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF=
如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF= 如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )
如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )