题目内容
正方形面积为36，则对角线的长为
- A.6
- B.
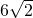
- C.9
- D.
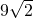
B
分析：根据对角线互相垂直的四边形的面积等于对角线乘积的一半，且正方形对角线相等，列方程解答即可．
解答：设对角线长是x．则有
x2=36，
解得x=6
．
故选B．
点评：本题考查了正方形的性质，注意结论：对角线互相垂直的四边形的面积等于对角线乘积的一半．此题也可首先根据面积求得正方形的边长，再根据勾股定理进行求解．
分析：根据对角线互相垂直的四边形的面积等于对角线乘积的一半，且正方形对角线相等，列方程解答即可．
解答：设对角线长是x．则有
x2=36，解得x=6
．故选B．
点评：本题考查了正方形的性质，注意结论：对角线互相垂直的四边形的面积等于对角线乘积的一半．此题也可首先根据面积求得正方形的边长，再根据勾股定理进行求解．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
77、阅读材料后再解答问题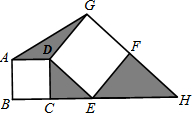
（2012•永嘉县一模）如图，C是线段BE上一点，四边形ABCD是正方形，四边形DEFG也是正方形，BE和GF的延长线相交于点H，连接AG，若正方形ABCD的面积16，正方形DEFG的面积为36，则图中三个阴影三角形的面积之和等于