Question

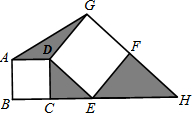（2012•永嘉县一模）如图，C是线段BE上一点，四边形ABCD是正方形，四边形DEFG也是正方形，BE和GF的延长线相交于点H，连接AG，若正方形ABCD的面积16，正方形DEFG的面积为36，则图中三个阴影三角形的面积之和等于

17

5

．

Answer 1

分析：过G作GM⊥AD交AD的延长线与M，根据正方形的性质得到DG=DE=EF=6，DC=4，利用勾股定理计算出CE=2

5

，易证Rt△DEC≌Rt△DGM，得到GM=CE；易证得Rt△DCE∽Rt△DFH，则CE：FH=DC：EF，即2

5

：FH=4：6，求得FH=3

5

，于是有S_{三个阴影三角形的面积}=

1

2

AD•GM+

1

2

DC•CE+

1

2

EF•FH，代值计算即可．

解答：解：过G作GM⊥AD交AD的延长线与M，如图，
∵正方形ABCD的面积16，正方形DEFG的面积为36，
∴DG=DE=EF=6，DC=4，
在Rt△DCE中，CE=

DE2-CE2

=2

5

，
∵∠1+∠2=90°，∠1+∠3=90°，
∴∠2=∠3，
又∵∠3=∠4，
∴∠2=∠4，
∴Rt△DEC≌Rt△DGM，
∴GM=CE；
∵∠5=∠6，
∴Rt△DCE∽Rt△DFH，
∴CE：FH=DC：EF，即2

5

：FH=4：6，
∴FH=3

5

，
∴S_{三个阴影三角形的面积}=

1

2

AD•GM+

1

2

DC•CE+

1

2

EF•FH
=

1

2

×4×2

5

×2+

1

2

×6×3

5

=17

5

．
故答案为17

5

．

点评：本题考查了相似三角形的判定与性质：有一组锐角对应相等的两直角三角形相似；相似三角形对应边的比相等．也考查了全等三角形的判定与性质、勾股定理以及正方形的性质．