题目内容
在如图所示的直角坐标系中，∠POx=120°，且OP=4，则点P的坐标是________．
（-2，2
）
分析：过点P作PA⊥x轴于A，然后求出∠POA，再解直角三角形求出OA，PA，然后根据点P在第二象限写出坐标即可．
解答：
解：如图，过点P作PA⊥x轴于A，
∵∠POx=120°，
∴∠POA=180°-120°=60°，
∵OP=4，
∴OA=OP•cos60°=4×
=2，
PA=OP•sin60°=4×
=2，
∴点P的坐标是（-2，2）．
故答案为：（-2，2）．
点评：本题考查了坐标与图形性质，主要利用了解直角三角形以及第二象限内点的坐标特征，作辅助线构造出直角三角形是解题关键．
）分析：过点P作PA⊥x轴于A，然后求出∠POA，再解直角三角形求出OA，PA，然后根据点P在第二象限写出坐标即可．
解答：
解：如图，过点P作PA⊥x轴于A，∵∠POx=120°，
∴∠POA=180°-120°=60°，
∵OP=4，
∴OA=OP•cos60°=4×
=2，PA=OP•sin60°=4×
=2，∴点P的坐标是（-2，2
）．故答案为：（-2，2
）．点评：本题考查了坐标与图形性质，主要利用了解直角三角形以及第二象限内点的坐标特征，作辅助线构造出直角三角形是解题关键．
练习册系列答案
相关题目
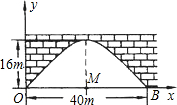如图，有一个抛物线的拱形立交桥，这个桥拱的最大高度为16m，跨度为40m，现把它放在如图所示的直角坐标系里，若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶，铁柱应取多长？
